Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные характеристики звуковых волн.Содержание книги
Поиск на нашем сайте
Основные характеристики звуковых волн. Скорость звука. К основным характеристикам звуковых волн относят скорость звука, его интенсивность – это объективные характеристики звуковых волн, высоту тона, громкость относят к субъективным характеристикам. Субъективные характеристики зависят в большой мере от восприятия звука конкретным человеком, а не от физических характеристик звука. Измерение скорости звука в твердых телах, жидкостях и газах указывают на то, что скорость не зависит от частоты колебаний или длины звуковой волны, т.е. для звуковых волн не характерна дисперсия. В твердых телах могут распространяться продольные и поперечные волны, скорость распространения которых находят с помощью формул: где Е – модуль Юнга, G – модуль сдвига в твердых телах. В твердых телах скорость распространения продольных волн почти в два раза больше чем скорость распространения поперечных волн. В жидкостях и газах могут распространяться лишь продольные волны. Скорость звука в воде находят за формулой:
где K- модуль объемного сжатия вещества. В жидкостях при возрастании температуры скорость звука возрастает, что связано с уменьшением коэффициента объемного сжатия жидкости. Для газов выведена формула, которая связывает их давление с плотностью:
впервые эту формулу для нахождения скорости звука в газах использовал И. Ньютон. Из формулы (1.1) видно, что скорость распространения звука в газах не зависит от температуры, она также не зависит от давления, поскольку при возрастании давления возрастает и плотность газа. Формуле (1.1) можно придать и более рациональный вид: на основе уравнения Менделеева – Клапейрона
тогда скорость звука будет равна:
Формула (1.2) носит название формулы Ньютона. Рассчитанная с ее помощью скорость звука в воздухе составляет при 273К 280 м/с. Реальная же экспериментальная скорость составляет 330 м/с. Этот результат значительно отличается от теоретического и причину этого установил Лаплас. Он показал, что распространение звука в воздухе происходит адиабатно. Звуковые волны в газах распространяются так быстро, что, что созданные локальные изменения объема и давления в газовой среде происходят без теплообмена с окружающей средой. Лаплас вывел уравнение для нахождения скорости звука в газах:
(1.3) .Формула (1.3) получила название формулы Лапласа.
Электромагнитные волны. Виды электромагнитных волн. Электромагнитная волна - процесс распространения электромагнитного поля в пространстве. Электромагнитная волна представляет собой процесс последовательного, взаимосвязанного изменения векторов напряжённости электрического и магнитного полей, направленных перпендикулярно лучу распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля. Для систематизации всех видов излучений составлена единая шкала электромагнитных волн: λ, м v, Гц тип волн источники 10 11-106 3·10 –3 - 3·10 2 низкочастотные волны генераторы переменного тока 10 5 -10–6 3·10 3 - 3·10 14 радиоволны открытый колебательный контур 10–3-10–6 3·10 11 - 3·10 14 инфракрасное излучение нагретые тела (7.5-3.9) ·10 -7 (4 – 8)·10 14 видимый свет нагретые тела 10 -7 -10-9 3·10 15 - 3 ·10 17 ультрафиолетовое излучение нагретые тела 10 –9-10-12 3·10 17 - 3·10 20 рентгеновское излучение рентгеновские трубки 10 -11-10-13 3·1019 - 3·10 21 g -излучение радиоактивный распад ядер элементов
Законы теплового излучения 1. Закон Кирхгофа. Тепловое излучение является равновесным - сколько энергии излучается телом, столь ее им и поглощается. Для трех тел, находящихся в замкнутой полости можно записать:
Указанное соотношение будет верным и тогда, когда одно из тел будет АЧ:
Т.к. для АЧТ αλT. Это закон Кирхгофа: отношение спектральной плотности энергетической светимости тела к его монохроматическому коэффициенту поглощения (при определенной температуре и для определенной длины волны) не зависит от природы тела и равно для всех тел спектральной плотности энергетической светимости при тех же самых температуре и длине волны. Следствия из закона Кирхгофа: 1. Спектральная энергетическая светимость АЧТ является универсальной функцией длины волны и температуры тела. 2. Спектральная энергетическая светимость АЧТ наибольшая. 3. Спектральная энергетическая светимость произвольного тела равна произведению его коэффициента поглощения на спектральную энергетическую светимость абсолютно черного тела.
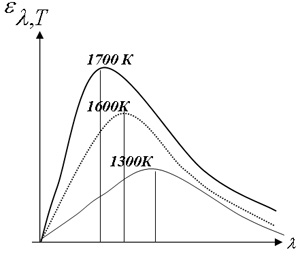
4. Любое тело при данной температуре излучает волны той же длины волны, которое оно излучает при данной температуре. Систематическое изучение спектров ряда элементов позволило Кирхгофу и Бунзену установить однозначную связь между спектрами поглощения и излучения газов и индивидуальностью соответствующих атомов. Так был предложен спектральный анализ, с помощью которого можно выявить вещества, концентрация которых составляет 0,1нм. Распределение спектральной плотности энергетической светимости для абсолютно черного тела, серого тела, произвольного тела. Последняя кривая имеет несколько максимумов и минимумов, что указывает на избирательность излучения и поглощения таких тел.
Закон Стефана-Больцмана. В 1879 году австрийские ученые Йозеф Стефан (экспериментально для произвольного тела) и Людвиг Больцман (теоретически для АЧТ) установили, что общая энергетическая светимость во всем диапазоне длин волн пропорциональна четвертой степени абсолютной температуры тела:
Закон Вина. Немецкий физик Вильгельм Вин в 1893 году сформулировал закон, который определяет положение максимума спектральной плотности энергетической светимости тела в спектре излучения АЧТ в зависимости от температуры. Согласно закону, длина волны λmax, на которую приходится максимум спектральной плотности энергетической светимости АЧТ, обратно пропорционален его абсолютной температуре Т: λmax = в/t, где в = 2,9*10-3 м·К- постоянная Вина. Таким образом, при увеличении температуры изменяется не только полная энергия излучения, но и сама форма кривой распределения спектральной плотности энергетической светимости. Максимум спектральной плотности при увеличении температуры смещается в сторону более коротких длин волн. Поэтому закон Вина называют законом смещения. Закон Вина применяется в оптической пирометрии - метода определения температуры по спектру излучения сильно нагретых тел, которые отдалены от наблюдателя. Именно этим методом впервые была определена температура Солнца (для 470нм Т=6160К).
Представленные законы не позволяли теоретически найти уравнения распределения спектральной плотности энергетической светимости по длинам волн. Труды Релея и Джинса, в которых ученые исследовали спектральный состав излучения АЧТ на основе законов классической физики, привели к принципиальным трудностям, названных ультрафиолетовой катастрофой. В диапазоне УФ-волн энергетическая светимость АЧТ должна была достигать бесконечности, хотя в опытах она уменьшалась к нулю. Эти результаты противоречили закону сохранения энергии.
4. Теория Планка. Немецкий ученый в 1900 году выдвинул гипотезу о том, что тела излучают не непрерывно, а отдельными порциями - квантами. Энергия кванта пропорциональна частоте излучения: E = hν = h·c/λ, где h = 6,63*10-34 Дж·с постоянная Планка. Руководствуясь представлениями о квантовом излучении АЧТ, он получил уравнение для спектральной плотности энергетической светимости АЧТ:
Эта формула находится в соответствии с опытными данными во всем интервале длин волн при всех температурах. Солнце - основной источник теплового излучения в природе. Солнечное излучение занимает широкий диапазон длин волн: от 0,1нм до 10м и более. 99% солнечной энергии приходится на диапазон от 280 до 6000нм. На единицу площади Земной поверхности приходится в горах от 800 до 1000 Вт/м2. До земной поверхности доходит одна двухмиллиардная часть тепла - 9,23 Дж/см2. На диапазон теплового излучения от 6000 до 500000нм приходится 0,4% энергии Солнца. В атмосфере Земли большая часть ИК-излучения поглощается молекулами воды, кислорода, азота, диоксида углерода. Радиодиапазон тоже большей частью поглощается атмосферой.
Количество энергии, которую приносят солнечные лучи за 1с на площадь в 1 кв.м, расположенную за пределами земной атмосферы на высоте 82 км перпендикулярную солнечным лучам называется солнечной постоянной. Она равна 1,4*103 Вт/м2. Спектральное распределение нормальной плотности потока солнечного излучения совпадает с таким для АЧТ при температуре 6000 градусов. Поэтому Солнце относительно теплового излучения - АЧТ.
Гипотеза де Бройля Идея об универсальной двойственности корпускулярных и волновых свойств всех объектов природы была впервые высказана Луи де Бройлем (в 1924 году) в качестве гипотезы о волновых свойствах частиц. Итак, мы знаем, что свету с частотой v и длиной волны λ соответствуют частицы — фотоны, обладающие энергией E = hv и импульсом p = h/λ. Де Бройль, в сущности, постулировал обратное. Гипотеза де Бройля. Движению каждой частицы соответствует распространение неко- торой волны. Частота и длина этой волны определяются энергией и импульсом частицы: v =E/h; λ =h/p Точно так же, любой волне с частотой v и длиной волны λотвечают частицы с энергией E = hv и импульсом p = h/λ. Чтобы лучше осмыслить гипотезу де Бройля, давайте обсудим дуализм «волна–частица» на примере электромагнитного излучения. В случае электромагнитных волн мы имеем следующую закономерность. По мере увеличения длины волны всё легче наблюдать волновые свойства излучения и всё труднее — корпускулярные. И наоборот, чем меньше длина волны, тем ярче выражены корпускулярные свойства излучения и тем труднее наблюдать его волновые свойства. Изменение соотношения корпускулярных и волновых свойств хорошо прослеживается при движении по известной вам шкале электромагнитных волн. Радиоволны. Длины волн здесь настолько велики, что корпускулярные свойства излучения практически не проявляются. Волновые свойства в этом диапазоне абсолютно доминируют. Длины волн могут составлять несколько метров или даже километров, так что волновая природа проявляется «сама собой» — радиоволны в процессе дифракции запросто огибают дома или горы. Излучение радиоволн и их взаимодействие с материальными объектами отлично описывается в рамках классической электродинамики.
Видимый свет и ультрафиолет. Это своего рода «переходная область»: в оптике мы можем наблюдать как волновые свойства света, так и корпускулярные.Однако в обоих случаях надо постараться. Так, длины волн видимого света много меньше размеров окружающих нас тел, поэтому в опытах по интерференции или дифракции света нужно создавать специальные условия (малость щелей или отверстий, удалённость экрана). В свою очередь, термин «красная граница фотоэффекта» также подчёркивает пограничность данного диапазона: фотоэффект начинается лишь при переходе через красную границу. Рентгеновское и гамма-излучение. Длины волн очень малы, и наблюдать волновые свойства излучения весьма затруднительно. Так, верхняя граница длин волн рентгеновского излучения составляет 10 нм; это лишь на два порядка превышает размер атома. Ясно, что дифракцию на «обычных» препятствиях при такой длине волны наблюдать невозможно. Однако в рентгеновский диапазон входят длины волн порядка размера атома и межатомных расстояний в кристалле (0;1 нм). Поэтому дифракция рентгеновских лучей наблюдается на «естественных» дифракционных решётках — кристаллических решётках твёрдых тел Энергия квантов в рентгеновском и гамма-диапазоне настолько велика, что излучение ведёт себя почти стопроцентно как поток частиц. Рассуждая по аналогии с электромагнитными волнами, можно заключить, что и частица будет проявлять волновые свойства тем лучше, чем больше её длина волны де Бройля (в масштабах данной ситуации). Так, мы совсем не наблюдаем волновых свойств у окружающих нас тел. (Видели вы, например, интерференцию движущихся автомобилей?) А почему? Давайте посчитаем длину дебройлевской волныобъекта массой 1 кг, движущегося со скоростью 1 м/с:
Это на 25 порядков меньше размера атома. Воображение отказывается представить себе столь малую величину. Разумеется, никакого волнового поведения у нашего объекта при таких условиях не обнаруживается — он стопроцентно ведёт себя как «частица», то есть как материальная точка классической механики.
12.Принцип неопределенностей Гейзенберга. В квантовой механике так называют принцип, дающий нижний (ненулевой) предел для произведения дисперсий величин, характеризующих состояние системы. Обычно принцип неопределённости иллюстрируется следующим образом. Рассмотрим ансамбль невзаимодействующих эквивалентных частиц, приготовленных в определённом состоянии, с каждой из которых производятся два последовательных измерения. Первое определяет импульс частицы, а второе, сразу после этого, её координату. Измерение импульса даст некоторое распределение с характерной дисперсией. Второе же измерение даст распределение значений, дисперсия которого d2q будет связана с дисперсией импульса d^2p так, что d^2q d^2p ≥h2/4 В общем смысле, соотношение неопределённости возникает между любыми переменными состояния, определяемыми некоммутирующими операторами. Это — один из краеугольных камней квантовой механики, который был открыт Вернером Гейзенбергом в 1927 г
Уравнение Шрёдингера. Для перехода от классическому к квантовому описанию достаточно заменить некоторые физические величины на соответствующие операторы (13.7). Для проверки работоспособности указанной идеи целесообразно осуществить указанную замену в функции Гамильтона (13.6), переписанной в нерелятивистском пределе (13.8). В результате получается нерелятивистское уравнение Шредингера, содержащее одно «лишнее» слагаемое, имеющее смысл энергии покоя электрона (13.9). Последнее легко устраняется переопределением уровня отсчета энергии за счет не изменяющего никаких физических результатов домножения всех волновых функций на одинаковый фазовый множитель (13.10).
Распределение Максвелла.
Работа газа при расширении. Работа при изменении объема газа Рис. 1. Газ оказывает давление на любую стенку сосуда. Если стенка подвижна (например, поршень на рис. 1), то сила давления F совершит работу A, переместив поршень на расстояние DL. Если DL невелико, то давление газа останется примерно постоянным. Тогда работа будет равна: A = F·DL·cosa = P·S·DL, где S - площадь поршня, a - угол между направлением силы и перемещением поршня (a = 0). Произведение S·DL равно изменению объема газа DV от начального V1 до конечного V2 значения, т.е. S·DL =DV = V1 - V2. Тогда A = P·(V2 - V1) = P·DV. В изобарном процессе расширения газа P = const. Следовательно, при любом сколь угодно большом увеличении объема сила давления газа на поршень будет постоянной, и формула работы сохранит свой вид A = P·(V2 - V1). Как видно из рисунка 2, работа газа при изобарном расширении равна площади под графиком процесса в координатах P, V.
Если в процессе расширения давление газа изменяется, то для вычисления работы можно воспользоваться графическим методом (см. рис. 3). Пусть процесс расширения имеет вид, изображенный на рисунке. При любом малом изменении объема DV работа равна площади малого прямоугольника (на рис. 3 он заштрихован). Полная работа равна сумме площадей всех малых прямоугольников и равна площади фигуры, ограниченной линией, представляющей собой график процесса.
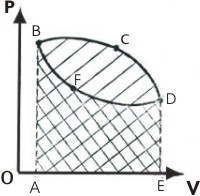
Рис. 3. При сжатии газа внешними силами перемещение поршня DL противоположно силе давления газа F, тогда работа газа будет отрицательной величиной (DV < 0). Работа внешней силы A' в данном случае будет положительной, а величина A' = - A. Работа газа в циклических процессах Совокупность термодинамических процессов, в результате которых система возвращается в исходное состояние называется циклом. Все тепловые машины (двигатели внутреннего сгорания, холодильные и паровые машины, и др.) работают циклически. Любой замкнутый цикл состоит из процессов расширения и сжатия (см. рис. 4). На участках BC и CD газ расширяется и совершает положительную работу A1, которая равна площади фигуры под линией ABCDE. В процессах DF и FB газ сжимается и совершает отрицательную работу A2, величина которой равна площади под линией ABFDE. Таким образом, полная работа газа равна площади цикла. В прямом цикле A > 0; в обратном цикле A < 0.
рис.4 Первый закон термодинамики. Первый закон термодинамики Внутренняя энергия может изменяться только под влиянием внешних воздействий, то есть в результате сообщения системе количества теплоты Q и совершения над ней работы (- А):
или
Это выражение представляет собой закон сохранения энергии в применении к макроскопическим системам и является математической формулировкой I-го начала термодинамики: количество тепла, сообщенное системе, идет на приращение внутренней энергии системы и на совершение системой работы над внешними телами. Если в изолированной системе (Q = A = 0) не происходит никаких превращений энергии, кроме теплообмена между телами, входящими в эту систему, то количество теплоты, отданное охлаждающимися при этом телами, равно количеству теплоты, полученному телами, которые нагреваются. Суммарная внутренняя энергия системы при этом не меняется.
Уравнение называется уравнением теплового баланса. Применим первое начало термодинамики для получения выражений для теплоемкости идеального газа. Теплоемкость системы численно равна количеству теплоты, которое необходимо сообщить системе, чтобы ее температура увеличилась на 1 Кельвин. Если система получила количество тепла ΔQ, и ее температура изменилась на ΔT, то теплоемкость этой системы будет равна: C = ΔQ/ΔT. (13) Если под системой понимается 1 моль вещества, то теплоемкость называется молярной и обозначается С, если под системой понимается единица массы вещества, то теплоемкость называется удельной и обозначается cуд: cуд = C/M. (14) Элементарное количество теплоты ΔQ, сообщаемое системе, представляющей собой
Внутреннюю энергию можно изменить двумя способами: путем передачи теплоты и путем совершения работы. При теплопередаче молекулы более нагретого тела передают часть своей энергии хаотического движения молекулам более холодного тела. Переданное количество теплоты является мерой изменения внутренней энергии каждого из тел: ΔU = Q. Принято считать, что Q > 0, если тело получает энергию, и Q < 0, если тело отдает свою энергию. При совершении механической работы должно происходить направленное перемещение тел под действием сил, например, перемещение поршня в цилиндре с газом. Если газ расширяется, то сила давления газа на поршень совершает положительную работу (A > 0) за счет внутренней энергии газа. Если внешние силы больше силы давления газа, то газ сжимается и работа газа будет отрицательной (A < 0), при этом внутренняя энергия увеличивается. В обоих случаях будет справедливо уравнение ΔU = – A. Если система одновременно совершает работу и получает или отдает теплоту, то изменение ее внутренней энергии ΔU = Q – A. Уравнение ΔU = Q – A называется первым законом термодинамики (или первым законом термодинамики). Изменение внутренней энергии термодинамической системы ΔU равно разности полученного количества теплоты Q и работы A, совершенной системой. Первый закон термодинамики является законом сохранения энергии для тепловых процессов. Согласно ему A = Q – ΔU. Этот закон говорит о том, что любая машина (любой двигатель) может совершать работу только за счет получения извне некоторого количества теплоты или уменьшения своей внутренней энергии. Многие изобретатели пытались построить машины, которые совершали бы работу, не тратя никакой энергии. Эти машины назывались вечными двигателями первого рода. Вечный двигатель первого рода не возможен – таков вывод из первого закона термодинамики. 20. Первый закон термодинамики (для изопроцессов). Применение первого закона термодинамики к изопроцессам Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характери- зующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается. 1. Изотермический процесс, T = const. Внутренняя энергия идеального газа зависит только от его температуры. Если темпера- тура газа не меняется, то не меняется и внутренняя энергия: U = 0. Тогда формула (3) даёт: Q = A: Всё подведённое к газу тепло идёт на совершение газом работы. 2. Изохорный процесс, V = const. Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: A = 0. Тогда первый закон термодинамики даёт: Q = U: Всё тепло, переданное газу, идёт на изменение его внутренней энергии. 3. Изобарный процесс, p = const. Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем: Q = U + pV: Уравнение Майера. Найдем связь между Ср и Сv идеального газа. Используя формулы запишем первое начало термодинамики в виде или Ср = Сv + R. (3.16) Формулу (3.16) называют уравнением Майера. Вывод: при изобарическом нагревании газа к нему подводится больше теплоты, чем при изохорическом. Практически изобарический процесс можно осуществить, например, при нагревании или охлаждении газа в цилиндре с подвижным поршнем, на который действует постоянная сила давления. Работу при изобарическом расширении идеального газа можно найти по формуле
или
Если при изменении температуры Ср не изменяется, то теплоту, сообщенную газу в изобарическом процессе, можно найти по формуле
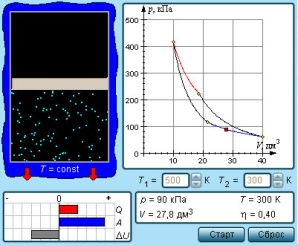
P-V диаграмма изобарического процесса приведена на рис. 3.4, где площадь прямоугольника (заштрихованная часть рисунка) численно равна работе газа в этом процессе. Цикл Карно Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T1. Газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A23 > 0. Температура газа при адиабатическом расширении падает до значения T2. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T2 < T1. Происходит процесс изотермического сжатия. Газ совершает работу A34 < 0 и отдает тепло Q2 < 0, равное произведенной работе A34. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T1, газ совершает работу A41 < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках: A = A12 + A23 + A34 + A41 На диаграмме (p, V) эта работа равна площади цикла. Процессы на всех участках цикла Карно предполагаются квазистатическими. В частности, оба изотермических участка (1–2 и 3–4) проводятся при бесконечно малой разности температур между рабочим телом (газом) и тепловым резервуаром (нагревателем или холодильником).Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли ΔU его внутренней энергии. Для одного моля газа A = –ΔU = –CV (T2 – T1), где T1 и T2 – начальная и конечная температуры газа. Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакам A23 = –A41 По определению, коэффициент полезного действия η цикла Карно есть
1.1. КПД цикла С. Карно выразил коэффициент полезного действия цикла через температуры нагревателя T1 и холодильника T2:
Цикл Карно замечателен тем, что на всех его участках отсутствует соприкосновение тел с различными температурами. Любое состояние рабочего тела (газа) на цикле является квазиравновесным, т. е. бесконечно близким к состоянию теплового равновесия с при конечной разности температур рабочего тела и окружающей среды (термостатов), когда тепло может передаваться без совершения работы. Поэтому цикл Карно – наиболее эффективный круговой процесс из всех возможных при заданных температурах нагревателя и холодильника: ηКарно = ηmax
Основные характеристики звуковых волн. Скорость звука. К основным характеристикам звуковых волн относят скорость звука, его интенсивность – это объективные характеристики звуковых волн, высоту тона, громкость относят к субъективным характеристикам. Субъективные характеристики зависят в большой мере от восприятия звука конкретным человеком, а не от физических характеристик звука. Измерение скорости звука в твердых телах, жидкостях и газах указывают на то, что скорость не зависит от частоты колебаний или длины звуковой волны, т.е. для звуковых волн не характерна дисперсия. В твердых телах могут распространяться продольные и поперечные волны, скорость распространения которых находят с помощью формул: где Е – модуль Юнга, G – модуль сдвига в твердых телах. В твердых телах скорость распространения продольных волн почти в два раза больше чем скорость распространения поперечных волн. В жидкостях и газах могут распространяться лишь продольные волны. Скорость звука в воде находят за формулой:
где K- модуль объемного сжатия вещества. В жидкостях при возрастании температуры скорость звука возрастает, что связано с уменьшением коэффициента объемного сжатия жидкости. Для газов выведена формула, которая связывает их давление с плотностью:
впервые эту формулу для нахождения скорости звука в газах использовал И. Ньютон. Из формулы (1.1) видно, что скорость распространения звука в газах не зависит от температуры, она также не зависит от давления, поскольку при возрастании давления возрастает и плотность газа. Формуле (1.1) можно придать и более рациональный вид: на основе уравнения Менделеева – Клапейрона
тогда скорость звука будет равна:
Формула (1.2) носит название формулы Ньютона. Рассчитанная с ее помощью скорость звука в воздухе составляет при 273К 280 м/с. Реальная же экспериментальная скорость составляет 330 м/с. Этот результат значительно отличается от теоретического и причину этого установил Лаплас. Он показал, что распространение звука в воздухе происходит адиабатно. Звуковые волны в газах распространяются так быстро, что, что созданные локальные изменения объема и давления в газовой среде происходят без теплообмена с окружающей средой. Лаплас вывел уравнение для нахождения скорости звука в газах:
(1.3) .Формула (1.3) получила название формулы Лапласа.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 710; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.71.102 (0.015 с.) |

 ,
, 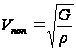
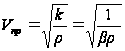

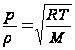









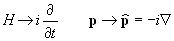 Способ перехода от классического к квантовому описанию.
Способ перехода от классического к квантовому описанию. Приближенное выражение для функции Гамильтона частицы, движущейся с малыми скоростями.
Приближенное выражение для функции Гамильтона частицы, движущейся с малыми скоростями. Нерелятивистское уравнение Шредингера.
Нерелятивистское уравнение Шредингера. Классическое уравнение Шредингера в случае отсутствия магнитного поля.
Классическое уравнение Шредингера в случае отсутствия магнитного поля. 17. Внутренняя энергия иде&чьного газа. Число степеней свободы.
17. Внутренняя энергия иде&чьного газа. Число степеней свободы.






 молей идеального газа, для изменения ее температуры от Т до Т + ΔT, равно:
молей идеального газа, для изменения ее температуры от Т до Т + ΔT, равно:
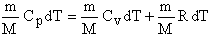
 (3.17)
(3.17) (3.18)
(3.18) (3.19)
(3.19)