
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель атома водорода по Бору.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Используя законы механики Ньютона и правило квантования, на основе которого определяются возможные стационарные состояния атома. Бор смог вычислить радиусы орбит электрона и энергии стационарных состояний атома. Минимальный радиус орбиты определяет размеры атома. На рисунке 12.4 значения энергий стационарных состояний (в элекгрон-вольтах1) отложены на вертикальной оси. Второй постулат Бора позволяет вычислить по известным значениям энергий стационарных состояний частоты излучений атома водорода. В атомной физике энергию принято выражать в электронвольтах (сокращенно эВ). 1 эВ равен энергии, приобретаемой электроном при прохождении им разности потенциалов 1 В: 1 эВ = 1,6. 10 Дж.
Теория Бора приводит к количественному согласию с экспериментом для значений этих частот. Все частоты излучений атома водорода составляют в своей совокупности ряд серий, каждая из которых образуется при переходах атома в одно из энергетических состояний со всех верхних энергетических состояний (состояний с большей энергией). Переходы в первое возбужденное состояние (на второй энергетический уровень) с верхних уровней образуют серию Бальмера. На рисунке 12.4 эти переходы изображены стрелками. Красная, зеленая и две синие линии в видимой части спектра водорода (см. рис. V, 3 на цветной вклейке) соответствуют переходам
Данная серия названа по имени швейцарского учителя И. Бальмера, который еще в 1885 г. на основе экспериментальных данных вывел простую формулу для определения частот видимой части спектра водорода. Поглощение света. Поглощение света — процесс, обратный излучению. Атом, поглощая свет, переходит из низших энергетических состояний в высшие. При этом он поглощает излучение той же самой частоты, которую излучает, переходя из высших энергетических состояний в низшие. На основе двух постулатов и правила квантования Бор определил радиус атома водорода и энергии стационарных состояний атома. Это позволило вычислить частоты излучаемых и поглощаемых атомом электромагнитных волн.
Корпускулярно-волновой дуализм. Волны де-Бройля. Корпускулярно-волновой дуализм — это физический принцип, утверждающий, что любой объект природы может вести себя и как частица, и как волна. С первым проявлением этого принципа мы столкнулись в предыдущем листке, когда говорили о двойственной, корпускулярно-волновой природе света. В явлениях интерференции и дифракции свет демонстрирует свою волновую природу. В явлении фотоэффекта свет выступает как дискретный поток частиц — фотонов. Гипотеза де Бройля Идея об универсальной двойственности корпускулярных и волновых свойств всех объектов природы была впервые высказана Луи де Бройлем (в 1924 году) в качестве гипотезы о волновых свойствах частиц. Итак, мы знаем, что свету с частотой v и длиной волны λ соответствуют частицы — фотоны, обладающие энергией E = hv и импульсом p = h/λ. Де Бройль, в сущности, постулировал обратное. Гипотеза де Бройля. Движению каждой частицы соответствует распространение неко- торой волны. Частота и длина этой волны определяются энергией и импульсом частицы: v =E/h; λ =h/p Точно так же, любой волне с частотой v и длиной волны λотвечают частицы с энергией E = hv и импульсом p = h/λ. Чтобы лучше осмыслить гипотезу де Бройля, давайте обсудим дуализм «волна–частица» на примере электромагнитного излучения. В случае электромагнитных волн мы имеем следующую закономерность. По мере увеличения длины волны всё легче наблюдать волновые свойства излучения и всё труднее — корпускулярные. И наоборот, чем меньше длина волны, тем ярче выражены корпускулярные свойства излучения и тем труднее наблюдать его волновые свойства. Изменение соотношения корпускулярных и волновых свойств хорошо прослеживается при движении по известной вам шкале электромагнитных волн. Радиоволны. Длины волн здесь настолько велики, что корпускулярные свойства излучения практически не проявляются. Волновые свойства в этом диапазоне абсолютно доминируют. Длины волн могут составлять несколько метров или даже километров, так что волновая природа проявляется «сама собой» — радиоволны в процессе дифракции запросто огибают дома или горы. Излучение радиоволн и их взаимодействие с материальными объектами отлично описывается в рамках классической электродинамики. Видимый свет и ультрафиолет. Это своего рода «переходная область»: в оптике мы можем наблюдать как волновые свойства света, так и корпускулярные.Однако в обоих случаях надо постараться. Так, длины волн видимого света много меньше размеров окружающих нас тел, поэтому в опытах по интерференции или дифракции света нужно создавать специальные условия (малость щелей или отверстий, удалённость экрана). В свою очередь, термин «красная граница фотоэффекта» также подчёркивает пограничность данного диапазона: фотоэффект начинается лишь при переходе через красную границу. Рентгеновское и гамма-излучение. Длины волн очень малы, и наблюдать волновые свойства излучения весьма затруднительно. Так, верхняя граница длин волн рентгеновского излучения составляет 10 нм; это лишь на два порядка превышает размер атома. Ясно, что дифракцию на «обычных» препятствиях при такой длине волны наблюдать невозможно. Однако в рентгеновский диапазон входят длины волн порядка размера атома и межатомных расстояний в кристалле (0;1 нм). Поэтому дифракция рентгеновских лучей наблюдается на «естественных» дифракционных решётках — кристаллических решётках твёрдых тел Энергия квантов в рентгеновском и гамма-диапазоне настолько велика, что излучение ведёт себя почти стопроцентно как поток частиц. Рассуждая по аналогии с электромагнитными волнами, можно заключить, что и частица будет проявлять волновые свойства тем лучше, чем больше её длина волны де Бройля (в масштабах данной ситуации). Так, мы совсем не наблюдаем волновых свойств у окружающих нас тел. (Видели вы, например, интерференцию движущихся автомобилей?) А почему? Давайте посчитаем длину дебройлевской волныобъекта массой 1 кг, движущегося со скоростью 1 м/с:
Это на 25 порядков меньше размера атома. Воображение отказывается представить себе столь малую величину. Разумеется, никакого волнового поведения у нашего объекта при таких условиях не обнаруживается — он стопроцентно ведёт себя как «частица», то есть как материальная точка классической механики.
12.Принцип неопределенностей Гейзенберга. В квантовой механике так называют принцип, дающий нижний (ненулевой) предел для произведения дисперсий величин, характеризующих состояние системы. Обычно принцип неопределённости иллюстрируется следующим образом. Рассмотрим ансамбль невзаимодействующих эквивалентных частиц, приготовленных в определённом состоянии, с каждой из которых производятся два последовательных измерения. Первое определяет импульс частицы, а второе, сразу после этого, её координату. Измерение импульса даст некоторое распределение с характерной дисперсией. Второе же измерение даст распределение значений, дисперсия которого d2q будет связана с дисперсией импульса d^2p так, что d^2q d^2p ≥h2/4 В общем смысле, соотношение неопределённости возникает между любыми переменными состояния, определяемыми некоммутирующими операторами. Это — один из краеугольных камней квантовой механики, который был открыт Вернером Гейзенбергом в 1927 г Уравнение Шрёдингера. Для перехода от классическому к квантовому описанию достаточно заменить некоторые физические величины на соответствующие операторы (13.7). Для проверки работоспособности указанной идеи целесообразно осуществить указанную замену в функции Гамильтона (13.6), переписанной в нерелятивистском пределе (13.8). В результате получается нерелятивистское уравнение Шредингера, содержащее одно «лишнее» слагаемое, имеющее смысл энергии покоя электрона (13.9). Последнее легко устраняется переопределением уровня отсчета энергии за счет не изменяющего никаких физических результатов домножения всех волновых функций на одинаковый фазовый множитель (13.10).
|
||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 596; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

 Модель атома водорода
Модель атома водорода

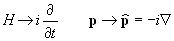 Способ перехода от классического к квантовому описанию.
Способ перехода от классического к квантовому описанию. Приближенное выражение для функции Гамильтона частицы, движущейся с малыми скоростями.
Приближенное выражение для функции Гамильтона частицы, движущейся с малыми скоростями. Нерелятивистское уравнение Шредингера.
Нерелятивистское уравнение Шредингера. Классическое уравнение Шредингера в случае отсутствия магнитного поля.
Классическое уравнение Шредингера в случае отсутствия магнитного поля.


