Элементарная теория атома водорода.

Планетарная модель атома. Атом построен из тяжёлого положительно заряженного ядра и окружающих его электронов. По классической механике такая система может находиться в равновесии лишь при условии, если электроны будут обращаться вокруг ядра по каким-то орбитам. Однако, с точки зрения классической электродинамики, такой атом был бы всё же неустойчив, так как при движении с ускорением электроны должны были бы излучать энергию в виде электромагнитных волн и, следовательно, постепенно падать к ядру. Вместе с тем и частота обращения при этих условиях должна была бы непрерывно меняться, и мы получили бы сплошной спектр вместо резких спектральных линий. Тот факт, что этого на самом деле не наблюдается, и атомы испускают резкие спектральные линии, указывает на их замечательную устойчивость, противоречащую классической электродинамике. Согласно планетарной модели Резерфорда атом следует рассматривать как ротатор, т. е. отрицательно заряженную частицу, обращающуюся по замкнутой орбите около положительного ядра. Постулат о существовании устойчивых стационарных состояний осцилляторов является необходимой предпосылкой для вывода правильной формулы излучения абсолютно чёрного тела. Бору принадлежит заслуга отчётливой формулировки этого положения и обобщения его на любые атомные системы. Тем самым впервые с полной ясностью была показана неприменимость классической физики к внутриатомным движениям). Идея о квантах, высказанная Планком в применении к обмену энергии между полем излучения и линейными осцилляторами, приобрела универсальное значение как выражение наиболее характерной особенности процессов внутриатомного мира. В основу развитой Бором квантовой теории строения атома положены следующие 2 постулата. 1. Из бесконечного множества электронных орбит, возможных с точки зрения классической механики, осуществляются в действительности только некоторые дискретные орбиты, удовлетворяющие определенным квантовым условиям. Электрон, находящийся на одной из этих орбит, несмотря на то, что он движется с ускорением, не излучает электромагнитных волн (света).2. Излучение испускается или поглощается в виде светового кванта энергии при переходе электрона из одного стационарного состояния в другое. Величина светового кванта равна разности энергий тех стационарных состояний, между которыми совершается квантовый скачок электрона: .

Спектральные закономерности. Линии в спектрах атомов расположены не беспорядочно, а объединяются в группы или, как их называют, серии линий. Отчетливее всего это обнаруживается в спектре водорода. Бальмер обнаружил, что длины волн (в видимой и близкой ультрафиолетовой области) серии линий водорода м/б точно представлены формулой , — константа, п = 3,4,5,… Если перейти от длины волны к частоте, получится формула , соответствующая серия спектральных линий водородного атома наз. серией Бальмера. Дальнейшие исследования показали, что в спектре водорода имеется еще несколько серий. В ультрафиолетовой части спектра находится серия Лаймана. Остальные серии лежат в инфракрасной области. Линии этих серий м/б представлены в виде аналогичных формул.

Серия Лаймана

серия Пашена ,

серия Брэкета

серия Фунда

 

Основы квантовой механики.

Квантовая теория изучает след. экспериментальные факты: процессы теплового излучения ачт, фотоэффект, эффект Комптона, люминесценцию, световое давление и т.д. В основе лежат 2 принципа: принцип дискретности (нек. физ.величины в опр.условиях м/т принимать только диск.(разр.) зн-я), принцип корпускулярно-волнового дуализма (микрообъект велет себя в одних условиях как волна, в др. как частица, являясь до опыта и тем и другим, а после опыта ни тем ни другим в классическом смысле слова). Под состоянием квантовой системы понимают набор характеристик (физ.величин) позволяющих выделить и идентифицировать конкретную физическую систему в конкретных физических условиях. Под наблюдаемой понимают любую физ.величину, которая м/б измерена в эксперименте, рез-ом которого д/б обязательно действительное число.

Под оператором подразумевают правило, посредством к-рого одной ф-ции () сопоставляется другая ф-ция ().Символически это запис-ся так: Здесь - символическое обозначение оператора. Под символом оператора скрывается совокупность действий, с помощью к-рых исходная ф-ция () превращается в другую ф-цию (). Наиболее важный класс операторов образуют линейные операторы, удовлетворяющие требованию для любой пары ф-ций и и любых постоянных комплексных чисел и . В рез-те применения оператора к ф-ции иногда получается вновь та же самая ф-ция, умноженная на некоторое число : (1). Если выполнено это соотношение, причем ф-ция удовлетворяет стандартным условиям (требованию конечности, непрерывности и однозначности ф-ции во всей области изменения независимых переменных) и условию квадратичной интегрируемости (требование чтобы интеграл от квадрата ф-ции или интеграл от квадрата ее модуля сущ-л, т.е. был конечным числом), то наз-ся собственной ф-цией оператора , а - его собственным значением, соответствующим собственной ф-ции . Если соотношение (1) выполнено, ф-ция удовлетворяет стандартным условиям, но не явл-ся квадратично интегрируемой, то наз-ся обобщенной собственной ф-цией оператора , а - точкой непрерывного (сплошного) спектра этого оператора. Совокупность всех собственных знач-й и всех точек непрерывного спектра оператора наз-ся его спектром.

Уравнение Шредингера - линейное дифференциальное уравнение в частных производных, описывающее изменение в пространстве (в общем случае, в конфигурационном пространстве) и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах

Здесь m – масса частицы i – мнимая единица, - Лапласиан.

 

Многоэлектронные атомы.

Многоэлектронными атомами наз-ся атомы с двумя и более электронами.

Ур-е Шредингера для многоэл. атомов:

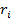где - расстояние i-ого электрона от ядра, 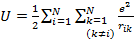- потенц. энергия взаимод-я м\у всеми N электронами атома; для нейтрального атома N=Z; - потенциальная энергия взаимод-я i-ого электрона с ядром, Е – полная энергия атома. Ур-е Шредингера для многоэлектронного атома м\б решено только приближенными методами, прежде всего методами теории возмущений. В основе реш-я лежит представление энергии взаимод-я м\у электронами U как малого возмущения по сравнению с энергией взаимод-я электронов с ядром. В кач-ве нулевого приближения получ-ся собственные знач-я и собственные ф-ции , соответсв-щие реш-ю с U=0:

где означает произвед-е N волн. ф-ций Реш-е ур-я Шредингера методами теории возмущений практически возможно только при малых знач-ях N.

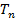Частота, соотв-щая границе серии, наз-ся термом и обозн-ся : (для водорода), R – постоянная Ридберга. Терм для изоэлектронного водороду иона: Обознач-я термов, к-рым соотв-ют различные l: l 0 1 2 3 4 Терм s p d f g. Буквы s,p,d,f соотв-ют английским наименованиям спектральный серий атомов с одним внешним электроном; s-внешняя, p-главная, d- диффузная f-фундаментальная. Правила отбора для орбитального квант. числа:

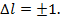
Атом гелия. Ур-е Шредингера для N=2: где 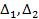- оператора Лапласа, Е – полная энергия атома, и 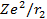- потенциальные энергии взаимод-я каждого из электронов с ядром, - расстояние м\у электронами, - энергия взаимод-я м\у электроноами. Уровни энергии и собственные ф-ции в нулевом приближении, в к-ром пренебрегается взаимод-ем электронов: 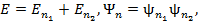где и -водородоподобная волн. ф-ция электрона. В первом приближении теории возмущений нормальное состояние атома гелия вычисл-ся с учетом энергии взаимного отталкивания электронов, описыв-х волн. ф-циями нормального состояния водородоподобного типа. 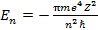Полная энергия основного состояния двухэлектронной системы в нулевом приближении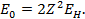: В первом приближении:

где - энергия атома водорода в нормальном состоянии.