
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение молекул по компонентам скоростей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Распределение Максвелла для вектора скорости
Это распределение имеет форму нормального распределения. Как и следует ожидать для покоящегося газа, средняя скорость в любом направлении равна нулю. Экспериментальная проверка распределения Максвелла. Схема опыта Ламмерта. 1-быстро вращающиеся диски, 2-узкие щели, 3-печь, 4-коллиматор, 5-траектория молекул, 6-детектор. При вращении дисков с постоянной угловой скоростью Меняя угловую скорость вращения дисков можно было отбирать из пучка молекулы, имеющие определенную скорость Таким способом удалось экспериментально проверить статистический закон распределения молекул по скоростям Распределение Больцмана — распределение вероятностей различных энергетических состояний идеальной термодинамической системы (идеальный газ атомов или молекул) в условиях термодинамического равновесия. Согласно распределению Больцмана среднее число частиц с полной энергией
Где
Барометрическая формула. Таким образом, зависимость атмосферного давления от высоты выражается формулой:
Броуновское движение. Длина свободного пробега. Частота соударений. Теорема о равномерном распределении кинетической энергии по степеням свободы. Характер движения броуновских частиц. Стохастические дифференциальные уравнения. Уравнение Смолуховского. Опыты Перрена по определению числа Авогадро. Броуновское движение – это беспорядочное непрерывное движение малых взвешенных частиц в жидкости или в газе, которое не зависит от внешних причин и оказывается проявлением внутреннего движения вещества. Броуновские частицы совершают движение под влиянием беспорядочных ударов молеул. Длина свободного пробега - с редняя длина пути, проходимого частицей между двумя последовательными соударениями с др. частицами. Это случайная величина Молекулы от столкновения до столкновения движутся равномерно и прямолинейно.Если за 1 сек молекула проходит в среднем путь равный скорости v, испытывая при этом ν упругих соударений с такими же молекулами, то средняя длина свободного пробега Частота соударений. В действительности все молекулы движутся, вследствие чего число соударений определяется средней скоростью движения молекул по отношению друг к другу. Как показывает соответствующий расчет, средняя скорость относительно движения молекул в Теорема о равномерном распределении кинетической энергии по степеням свободы. Число степеней свободы i - число независимых переменных (координат), которые необходимо задать для определения положения тела в пространстве.Средняя энергия приходящаяся на одну степень свободы: Характер движения броуновских частиц. Причина броуновского движения заключается в том, что при достаточно малых размерах частиц импульсы, сообщаемые частице ударяющимися о нее с разных сторон молекулами, оказываются нескомпенсированными. О частицу заметных размеров ударяется одновременно большое число молекул, так что суммарный результат ударов молекул достаточно хорошо усредняется. При малых размерах частицы начинают проявляться отклонения скоростей отдельных молекул и числа ударяющихся молекул от средних значений. Если скорость или число молекул, ударяющихся о частицу с одной стороны, окажется иной, чем для молекул, ударяющихся с другой стороны, то результирующий импульс, сообщаемый частице, будет отличен от нуля и частица начнет двигаться в соответствующем направлении. В следующий момент результирующий импульс имеет иное направление. Следовательно, частица будет все время перемещаться беспорядочным образом. Стохастические дифференциальные уравнения - дифференциальное уравнение, в котором один член или более представляют собой случайный процесс. Уравнение Смолуховского — кинетическое уравнение, описывающее эволюцию функции распределения координат и скоростей частиц при одномерном броуновском движении
где Опыты Перрена по определению числа Авогадро. Взвешенные в жидкости очень мелкие твердые частицы находятся в состоянии непрестанного беспорядочного движения. Броуновское движение указывает на то, что достаточно малые частицы вовлекаются в совершаемое молекулами тепловое движение. Принимая участие в тепловом движении, такие частицы должны вести себя подобно гигантским молекулам, и на них должны распространяться закономерности кинетической теории, в частности закон распределения Больцмана. Основную трудность в опытах Перрена составляло приготовление одинаковых частиц и определение их массы. однородную эмульсию. Эмульсия помещалась в плоскую стеклянную кювету глубиной 0,1 мм и рассматривалась с помощью микроскопа. Перемещая микроскоп в вертикальном направлении, можно было исследовать распределение броуновских частиц по высоте. С помощью этой формулы по измеренным можно определить постоянную Больцмана k. Далее, разделив газовую постоянную R на k, можно было найти число Авогадро.
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.88.18 (0.007 с.) |

 — является произведением распределений для каждого из трех направлений:
— является произведением распределений для каждого из трех направлений:  , где распределение по одному направлению:
, где распределение по одному направлению:
 , через их прорези беспрепятственно проходили только атомы, имевшие скорость
, через их прорези беспрепятственно проходили только атомы, имевшие скорость 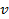 :
:  (5.75) где
(5.75) где 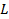 - расстояние между вращающимися дисками.
- расстояние между вращающимися дисками. равно
равно
 - кратность состояния частицы с энергией
- кратность состояния частицы с энергией  находится из условия, что сумма
находится из условия, что сумма  по всем возможным значениям
по всем возможным значениям  равна заданному полному числу частиц
равна заданному полному числу частиц  в системе (условие нормировки):
в системе (условие нормировки):

 , где n — число молекул в единице объёма (плотность газа), σ — эффективное поперечное сечение молекулы.
, где n — число молекул в единице объёма (плотность газа), σ — эффективное поперечное сечение молекулы.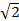 раз больше скорости <v> молекул относительно стенок сосуда. Поэтому среднее число столкновений за секунду будет равно
раз больше скорости <v> молекул относительно стенок сосуда. Поэтому среднее число столкновений за секунду будет равно 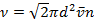 .
. , у одноатомной молекулы i=3, тогда
, у одноатомной молекулы i=3, тогда  , для двухатомной молекулы i=5, для трехатомной i=6. Т. о., на среднюю кинетическую энергию молекулы, имеющей i – степеней свободы, приходится
, для двухатомной молекулы i=5, для трехатомной i=6. Т. о., на среднюю кинетическую энергию молекулы, имеющей i – степеней свободы, приходится  .
. {\displaystyle {\frac {\partial P}{\partial t}}=\left[-{\frac {\partial }{\partial x}}v+{\frac {\partial }{\partial v}}\left(\gamma v-{\frac {F(x)}{m}}\right)+{\frac {\gamma k_{B}T}{m}}{\frac {\partial ^{2}}{\partial ^{2}v}}\right]P}
{\displaystyle {\frac {\partial P}{\partial t}}=\left[-{\frac {\partial }{\partial x}}v+{\frac {\partial }{\partial v}}\left(\gamma v-{\frac {F(x)}{m}}\right)+{\frac {\gamma k_{B}T}{m}}{\frac {\partial ^{2}}{\partial ^{2}v}}\right]P} - функция распределения броуновских частиц по координатам и скоростям, v — скорость,
- функция распределения броуновских частиц по координатам и скоростям, v — скорость,  - внешняя сила,
- внешняя сила,  - постоянная Больцмана, T — температура,
- постоянная Больцмана, T — температура, 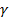 - параметр, характеризующий вязкость среды, в которой происходит броуновское движение. Уравнение Смолуховского является частным случаем уравнения Фоккера — Планка.
- параметр, характеризующий вязкость среды, в которой происходит броуновское движение. Уравнение Смолуховского является частным случаем уравнения Фоккера — Планка.


