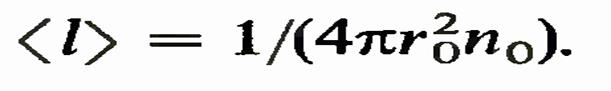Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Биноминальное распределение. Распределения Пуассона и Гаусса. Флуктуации.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Бином Ньютона выражается формулой Распределение Пуассона: В случае n>>m и np=m0=const можно воспользоваться формулой Стирлинга Распределение Гаусса: Прологарифмируем распределение Пуассона, получим вблизи точки m=m0, ограничиваясь квадратичным членом, получим Флуктуация: мерой флуктуации является стандартное отклонение от среднего значения. Роль флуктуации возрастает с уменьшением области, в которой эти флуктуации рассматриваются. В макроскопических системах статических флуктуаций незначительны. Относительная роль флуктуации уменьшается с увеличением области и среднего числа частиц в ней.
7.Распределение молекул по скоростям. Распределение Максвелла по вектору скорости. Распределение Максвелла по компонентам скорости. получено при следующих условиях: все молекулы имеют одинаковую температуру (газ равновесный); при соударениях молекул соблюдается условие детального равновесия, т.е. при соударении пары молекул, когда эти молекулы поменяли свои скорости, в газе всегда найдутся две другие молекулы, которые приобрели те же самые скорости, которые имелись в первой паре до соударения, иначе, число молекул, имеющих заданную скорость не меняется со временем; все молекулы одинаковые (имеют одинаковую массу и размер). Максвелл предположил, что число молекул газа, имеющих скорости в диапазоне коэффициента учтем, что абсолютному значению скорости имеет вид
Распределение Максвелла по абсолютному значению скорости. Характерные скорости. Распределение Максвелла по абсолютному значению скорости имеет вид
Характерные скорости Средняя арифметическая скорость Мы знаем среднюю квадратичную скорость. Вычислим среднюю арифметическую скорость по формуле
Нарисуем распределение Максвелла Распределение Максвелла
Наивероятнейшая скорость Видно, что распределение Максвелла имеет максимум. Найдем соответствующую этому максимуму скорость, которая называется наивероятнейшей скоростью. Используем условие обращения в нуль производной в соответствующей точке. Имеем
9.Приведенное распределение Максвелла. Число молекул в различных участках распределения Максвелла. Принцип детального равновесия. Приведенное распределение Введем переменную
Число молекул, имеющих скорости в заданном интервале Для нахождения числа молекул Δ N, имеющих скорости в диапазоне ϑ1<ϑ<ϑ2, следует найти интеграл
К сожалению, такой интеграл можно вычислить только численным способом. В случае скоростей из диапазона от ϑ до ϑ+Δϑ, где Δϑ<<ϑ, приближенно найдем
Численное вычисление дает
10.Число ударов молекул о стенку. Экспериментальная проверка распределения Максвелла. Границы применимости распределения Максвелла. Экспериментальная проверка Эксперимент Штерна Частота ударов о стенку Для нахождения частоты ударов молекул о стенку сосуда ν необходимо вычислить интеграл
где n – концентрация молекул, s – площадь стенки. При вычислении было учтено, что вклад вносят только молекулы, движущиеся в направлении стенки (находящейся на положительной части оси x) и имеющих направление скорости нормальное, по отношению к стенке.
11.Поперечное сечение.Средняя длина свободного пробега.Частотоа столкновений.Экспериментальное определение длины свободного пробега молекул. Поперечное сечение. При движении в газе молекула испытывает столкновения, в результате чего она изменяет направление своего движения. Вероятность столкновения с конкретным результатом описывается с помощью понятия поперечного сечения. Пусть падающая частица попадает на площадь S объема, в котором расположены частицы-мишени с концентрацией n0. В слое толщины dx находится число частиц-мишеней n0Sdx, а сумма их поперечных сечений, которая как бы закрывает часть площади S, равна dS =
Частота столкновений. Падающая частица движется со средней скоростью <v>> и, следовательно, проходит длину среднего свободного пробега за время t= <l>/<v>. Поэтому средняя частота столкновений (среднее число столкновений за 1 с) равна
При рассмотрении столкновений одинаковых молекул в газах их чаще всего представляют в виде твердых шаров. Пусть молекулы-мишени неподвижны, а падающая на них молекула движется со скоростью <v>>. Очевидно, падающая молекула, пройдя расстояние х, столкнется со всеми молекулами-мишенями, центры которых находятся в круглом цилиндре с радиусом основания 2г0 и высотой х. Средняя длина свободного пробега равна высоте цилиндра, в котором в среднем находится одна молекула-мишень. Поэтому для определения среднего свободного пробега получаем уравнение
из которого следует, что Частота соударений между молекулами на основании равна
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 916; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.78.87 (0.009 с.) |

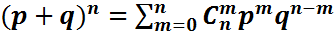 Если p+q=1 и p, q>0, то бином Ньютона превращается в биноминальное распределение
Если p+q=1 и p, q>0, то бином Ньютона превращается в биноминальное распределение 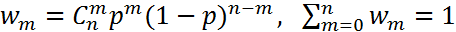 Биноминальное распределение соответствует распределению вероятности того, что при n испытаниях рассматриваемое событие (имеющее вероятность p) реализуется m раз. В случае больших n и m воспользуемся формулой Стирлинга, получим
Биноминальное распределение соответствует распределению вероятности того, что при n испытаниях рассматриваемое событие (имеющее вероятность p) реализуется m раз. В случае больших n и m воспользуемся формулой Стирлинга, получим  Дифференцируя это выражение по m и приравнивая к нулю, получим
Дифференцируя это выражение по m и приравнивая к нулю, получим 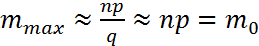 где m0 – соответствует максимуму биноминального распределения.
где m0 – соответствует максимуму биноминального распределения. В пределе получим
В пределе получим  - распределение Пуассона.
- распределение Пуассона.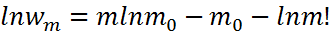 или пользуясь формулой Стирлинга
или пользуясь формулой Стирлинга  Разложим последнее выражение в ряд Тейлора
Разложим последнее выражение в ряд Тейлора ,
,  - называется распределением Гаусса.
- называется распределением Гаусса.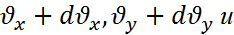
 равно
равно  Для нахождения нормировочного
Для нахождения нормировочного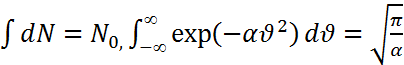 . Распределение Максвелла покомпонентам скорости имеет вид
. Распределение Максвелла покомпонентам скорости имеет вид 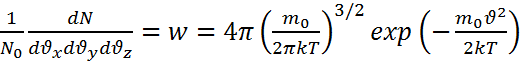 , и распределение Максвелла по
, и распределение Максвелла по




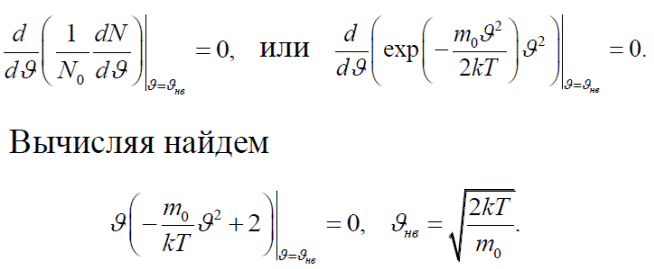
 Тогда распределение Максвелла примет т.н. приведенный вид
Тогда распределение Максвелла примет т.н. приведенный вид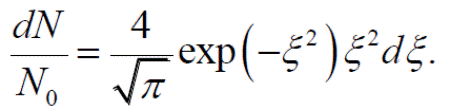


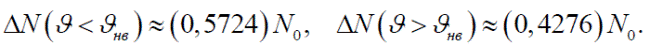
 Эксперимент Элдриджа
Эксперимент Элдриджа
 n0S dx. Отсюда следует, что вероятность того, что падающая частица попадет в одну из частиц-мишеней в слое dx, равна1
n0S dx. Отсюда следует, что вероятность того, что падающая частица попадет в одну из частиц-мишеней в слое dx, равна1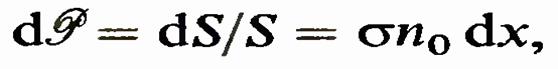 где использовано определение вероятности. Это есть определение поперечного сечения а рассматриваемого процесса. Средняя длина свободного пробега. Величины
где использовано определение вероятности. Это есть определение поперечного сечения а рассматриваемого процесса. Средняя длина свободного пробега. Величины  , из которого следует, что
, из которого следует, что