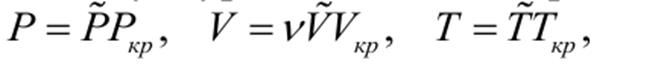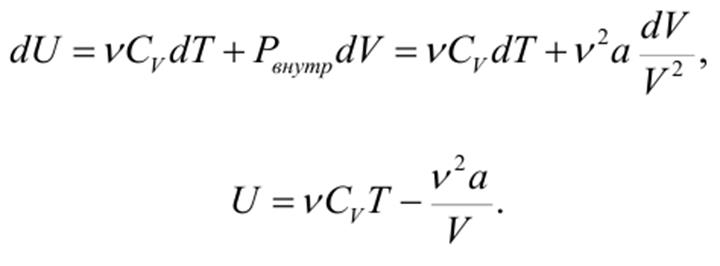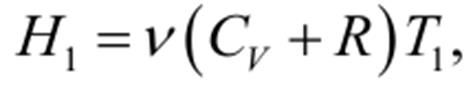Приведенное уравнения Ван-дер-Вальса. Внутрения энергия газа ванн-дер-Вальса.

Приведенное уравнение ВдВ Делая замену в уравнении Ван-дер-Ваальса:

Получим приведенное уравнение Ван-дер-Ваальса

Видно, что при выборе в качестве единиц критических параметров вещества уравнение ВдВ принимает вид, одинаковый для всех веществ. Отсюда можно заключить, что и поведение различных веществ (в приведенных величинах) одинаково. Это утверждение называется законом соответственных состояний. Формулируется он так: если два приведенных параметра вещества одинаковы, то и третий параметр одинаков. Однако надо заметить, что закон соответственных состояний все же не соблюдается для реальных газов и жидкостей.

Отличие результатов

К сожалению, простая теория, связанная с использованием уравнения ВдВ не всегда адекватно описывает реальную ситуацию. Основные отличия следующие. 1. Для данного вещества постоянные а и b в уравнении Ван-дер-Ваальса должны быть независимыми от температуры. В действительности же они зависят от температуры. 2. Из соотношения критических параметров следует, что величина

должна быть универсальной постоянной для всех веществ. В действительности же она изменяется.Например, для воды она равна 0,23, а для гелия 0,31. 3. Соотношение V0,кр=3b не соблюдается. Более точным соотношением является V0,кр≈2b. 4. В области двухфазных состояний уравнение Ван-дер-Ваальса не обосновано теоретически и дает расхождения с экспериментом.

Внутренняя энергия газа ВдВ

Взаимодействие между молекулами газа ВдВ обусловливает их взаимную потенциальную энергию. Поэтому, наряду с величиной νCVdT, в элементарное изменение внутренней энергии газа dU должна входить работа против внутренних сил притяжения dA’= Pвнутр dV. Следовательно, для газа Ван-дер-Ваальса

 

 

 

Эффект Джоуля-Томсана

Пропуская реальный газ по теплоизолированной трубке с пористой перегородкой, Джоуль и Томсон обнаружили, что при расширении, которым сопровождается прохождение газа через перегородку, температура его несколько изменяется. В зависимости от начальных давления и температуры изменениеприращения температуры ΔT имеет различные знаки («плюс» или «минус»). Это явление получило название эффекта Джоуля-Томсона. Если температура газа понижается (ΔT <0), эффект называется положительным; если газ нагревается (ΔT >0), эффект называется отрицательным. Пусть индексом «1» выделены, параметры, описывающие начальное состояния газа, а индексом «2» обозначим параметры, соответствующие его конечному состоянию (после расширения) Можно доказать, что в эксперименте Джоуля и Томсона сохраняется энтальпия, т.е. выполняется условие

Таким образом, знак эффекта Джоуля-Томсона

определяется знаком выражения, стоящего в квадратных

скобках.

- эффект получается нулевым. Следует заметить, что эффект Джоуля-Томсона всецело обусловлен отклонениями газа от идеальности. Для идеального газа энтальпия H1 имеет вид

а условие равенства энтальпий принимает вид

Т.е. эффект является нулевым.

 

Переход из газообразного в жидкое. Экспериментальные изотермы.

Насыщенный пар

Если покинувшие жидкость молекулы удаляются из пространства вблизи поверхности жидкости, то в конце концов вся жидкость испарится. Если же молекулы, покинувшие жидкость, не удаляются, а удерживаются в замкнутом объеме около поверхности жидкости, то дальнейший процесс развивается по-другому. Покинувшие жидкость молекулы образуют пар. Молекулы пара, попавшие в область вблизи поверхности жидкости, силами притяжения втягиваются в жидкость. Таким образом, скорость испарения уменьшается. При дальнейшем увеличении плотности пара достигается такая ситуация, когда число молекул, покидающих жидкость за некоторое время, равно числу молекул, возвращающихся в жидкость за то же время. Наступает состояние динамического равновесия. Пар в состоянии динамического равновесия с жидкостью называется насыщенным. С увеличением плотности насыщенных паров поверхностное натяжение жидкости уменьшается, поскольку силы, направленные внутрь жидкости, уменьшаются ввиду роста противоположно направленных сил со стороны насыщенного пара. Отсюда же следует, что скрытая теплота парообразования с повышением температуры уменьшается. При критической температуре плотность насыщенных паров становится равной плотности жидкости и различие между ними исчезает. Это означает, что и поверхность исчезает, и, следовательно, поверхностное натяжение и скрытая теплота парообразования при критической температуре обращаются в нуль. При конденсации пара в жидкость его молекулы взаимно притягиваются, в результате чего их скорости, а следовательно, и их кинетическая энергия возрастают. Это ведет к нагреванию образующейся жидкости: теплота,

затраченная при испарении, отдается обратно при конденсации пара.