
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Величин. Среднее по ансамблю и среднее по времени. Эргодическая среднее значение дискретной и непрерывной случайных гипотеза.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Среднее значение зависит от переменной, по которой производится усреднение. Дискретная величина:
Непрерывная величина:
Вычисление средних по ансамблю: возьмём некоторую величину, связанную с конкретной частицей, например квадрат ее координаты. Расположение системы координат может быть произвольным, необходимо лишь, чтобы оно было одинаковым относительно всех систем ансамбля. Будем индексом i нумеровать координату частицы в i-й системе статического ансамбля. Тогда, по определению средней величины, получим: Вычисление средних по времени: по определению ср по времени:
Эргодическая гипотеза. Утверждает что в состоянии равновесия средняя величина по ансамблю равна средней величине по времени.
5.Методы описания систем многих частиц. Микроскопическое состояние.Равновесное состояние.Статистический ансамбль систем.Системой называется конечная область пространства с находящимися в ней физическими объектами исследования. Граница системы может быть как материальной (например, стенка сосуда), так и воображаемой, проведенной в пространстве мысленно. Она может быть неподвижной или движущейся. Граница может быть проницаемой или непроницаемой для вещества, через нее либо невозможен, либо возможен транспорт энергии, причем в последнем случае она классифицируется по формам энергии, которые через нее могут транспортироваться. Система характеризуется не только особенностями своей границы, но и физическими или химическими свойствами вещества, находящегося в занимаемой системой области пространства. Классификация систем по этим признакам будет даваться в книге по мере надобности. Первая система, с которой начинается рассмотрение, называется идеальным газом. Под идеальным газом понимается совокупность точечных частиц конечной массы, столкновение между которыми происходит по законам абсолютно упругого удара шаров, причем других способов взаимодействия между частицами нет, т. е. силы взаимодействия на конечном расстоянии отсутствуют. Макроскопическое состояние. Пусть в некотором объеме V заключен идеальный газ. Предположим, что удары частицы о стенки сосуда абсолютно упругие, а масса сосуда очень велика, благодаря чему состояние движения из-за ударов частиц по его стенкам не изменяется. Таким образом, заключенный в объеме V газ не обменивается энергией с находящимися вне объема V материальными телами, т. е. является изолированным. При этом условии газ в сосуде изолирован от каких- либо внешних воздействий и все, что с ним может произойти, происходит в результате внутренних причин. По прошествии достаточного промежутка времени, в течение которого система предоставлена самой себе, состояние газа станет стационарным и не будет изменяться со временем. Состояние газа, характеризуемое его давлением, температурой и объемом, называется макроскопическим. Равновесное состояние. Стационарное макроскопическое состояние газа, находящегося в изолированном от внешней среды объеме V, называется равновесным. При этом его макроскопические характеристики — давление, температура, объем — сохраняют свои постоянные значения во времени, причем давление и температура имеют постоянные значения во всех частях объема. Под частями объема имеют в виду достаточно большие части, в которых содержится очень большое число частиц. В определении равновесного состояния оговорка об изолированности системы существенна. Если система не изолирована, то возможно стационарное состояние, которое не является равновесным. Если, например, различные части стенки сосуда, в котором заключен газ, с помощью внешних источников теплаподдерживать при различной, но постоянной температуре, то в газе установится стационарное состояние, т. е. состояние, не изменяющееся со временем, однако оно не равновесное. В этом случае давление во всех частях объема одинаково, а температура во всех частях объема различна. Микроскопическое состояние. Наиболее полная информация о газе содержится в констатации положений и скоростей всех его частиц Пронумеруем частицы газа индексами i = 1, 2,... п, т. е. всего в рассматриваемом объеме имеется п частиц. Это число очень велико. Если объем L(3) = 1 см3, то при нормальных атмосферных условиях п = 2,7 -1019 частиц. Состояние газа, характеризуемое положениями и скоростями всех его частиц, называется микроскопическим. Следовательно, микроскопическое состояние газа характеризуется 6n числами: 3n координатами (xi yi zi,) всех частиц и 3n компонентами (vxi vyi, vzi) их скоростей. Эти числа следует рассматривать как случайные величины. Макроскопическое состояние характеризуется тремя величинами: давлением, темпе- ратурой и объемом, которые стационарном состоянии постоянны. Однако частицы газа в стационарном состоянии движутся и, следовательно, его микроскопические состояния беспрерывно изменяются. Таким образом, одному и тому же макроскопическому состоянию соответствует громадное множество микроскопических состояний Статистический ансамбль систем. Метод ансамбля систем удобен для анализа вопросов статистической физики. Возьмем очень большое число N совершенно одинаковых сосудов, каждый из которых имеет объем V. В каждом из сосудов находится одинаковое число п одинаковых частиц. Сосуд с заключенными в нем частицами называется статистической системой. Совокупность одинаковых статистических систем называется статистическим ансамблем. Нас не интересует, как движутся частицы и в каких точках соответствующего сосуда они находятся в некоторый начальный момент времени. Задача заключается в том, чтобы изучить микро- и макросостояния отдельных систем ансамбля через некоторый достаточно большой промежуток времени, причем «достаточный промежуток времени» понимается в только что разъясненном смысле. Из изложенного ясно, что одно и го же макроскопическое состояние осуществляется в большом числе систем ансамбля, находящихся в различных микроскопических состояниях..
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1742; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.69.74 (0.008 с.) |

 - среднее значение;
- среднее значение; 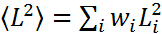 -квадрат среднего квадратичного значения;
-квадрат среднего квадратичного значения;  - условие нормировки. Полезные соотношения
- условие нормировки. Полезные соотношения 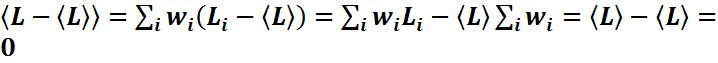 ;
; .
. - среднее значение;
- среднее значение;  - квадрат среднего квадратичного значения;
- квадрат среднего квадратичного значения;  - условие нормировки. Полезные соотношения
- условие нормировки. Полезные соотношения 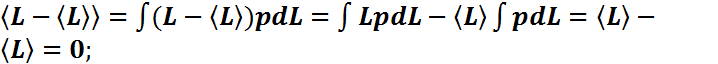

 В этом равенстве индекс а показывает, что вычисляемая величина является средней по ансамблю,
В этом равенстве индекс а показывает, что вычисляемая величина является средней по ансамблю,  -число систем в ансамбле;
-число систем в ансамбле;  -координата частицы в i-й системе ансамбля. Число ячеек в каждой системе ансамбля равно
-координата частицы в i-й системе ансамбля. Число ячеек в каждой системе ансамбля равно  , а число систем
, а число систем  )
)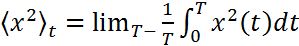 ; i- последовательные скачки частицы; xi – координата ячейки, в кот при своём движении частица переходит после i-го скачка, а
; i- последовательные скачки частицы; xi – координата ячейки, в кот при своём движении частица переходит после i-го скачка, а  -время пребывания частицы в этой ячейке после прибытия туда при i-м скачке.
-время пребывания частицы в этой ячейке после прибытия туда при i-м скачке. 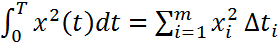 где m-число скачков в течении времени T.
где m-число скачков в течении времени T.  . При очень большом времени
. При очень большом времени 
 за время Т она в j-й ячейке проведёт время
за время Т она в j-й ячейке проведёт время  где сумма берётся по всем i соответствующим j-й ячейке. Значит вероятность
где сумма берётся по всем i соответствующим j-й ячейке. Значит вероятность  -продолжительность пребывания частицы в j-й ячейке относительно всего времени.
-продолжительность пребывания частицы в j-й ячейке относительно всего времени. -наз эргодической гипотезой. Её можно выразить иначе:
-наз эргодической гипотезой. Её можно выразить иначе:  т.е. среднее по ансамблю равно ср по времени. Эргодическая гипотеза предполагает, что в этой совокупности имеются все возможные микросостояния системы, которые только совместимы с пространственными возможностями движения частиц и с законом сохранения энергии (если рассматриваются также и распределения частиц по импульсам). Любая из систем ансамбля в течении достаточно продолжительного промежутка времени пройдёт все возможные микросостояния, причём её относительное время пребывания в каждом из микросостояний равно относительному числу систем в ансамбле, нах в этом микросостоянии. Следствием является то что средние по ансамблю равны средним по времени.
т.е. среднее по ансамблю равно ср по времени. Эргодическая гипотеза предполагает, что в этой совокупности имеются все возможные микросостояния системы, которые только совместимы с пространственными возможностями движения частиц и с законом сохранения энергии (если рассматриваются также и распределения частиц по импульсам). Любая из систем ансамбля в течении достаточно продолжительного промежутка времени пройдёт все возможные микросостояния, причём её относительное время пребывания в каждом из микросостояний равно относительному числу систем в ансамбле, нах в этом микросостоянии. Следствием является то что средние по ансамблю равны средним по времени.


