
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопроводность твердого телаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Коэффициент теплопроводности кристаллического твердого тела можно представить в виде где ϑ зв – скорость звука в твердом теле; lф – средняя длина свободного пробега фонона в твердом теле (фонон – квазичастица, являющаяся квантом (элементарной величиной) коллективных колебаний атомов в кристалле). Процессы переноса в жидкости Коэффициент диффузии (самодиффузии) в жидкости имеет такой же вид как и для твердого тела. При этом молекула жидкости находится не в узле кристаллической решетки, а в некотором «месте оседлой жизни». Перескочить молекуле из одного места в другое проще (требуется меньше энергии), чем для атома в узле кристаллической решетки. Явление теплопроводности в жидкости сложно, и каких-либо общих аналитических выражений пока не получено. Можно лишь сказать, что теплопроводность жидкостей лежит где то в середине между теплопроводности газа и теплопроводности твердого тела. Вязкость жидкости Коэффициент вязкости жидкости при постоянной температуре хорошо описывается формулой Бачинского где A и b – постоянные, определяемые свойствами жидкости (b – постоянная Ван-дер-Ваальса); V 0 – молярный объем жидкости. Зависимость вязкости от температуры дается формулой Френкеля
Физические явления в разреженных газах. Явления в сосудах, сообщающихся через пористую перегородку. Ультраразреженный газ Если длина свободного пробега молекул превышает линейные размеры сосуда, в котором заключен газ, то такой газ называют ультраразреженным. В таком газе молекулы не сталкиваются друг с другом, поэтому все явления переноса протекают иначе, чем в обычном идеальном газе. Молекулы сталкиваются только со стенками сосуда. Теплоперенос в ультраразреженном газе Пусть в газе имеются две пластинки с температурами T 1 и T 2. Тогда, для элементарно приращения тепла можно получить где S – площадь пластинки, а величина теплопроводности ультраразреженного газа. Видно, что эта величина пропорциональна плотности газа: с уменьшением плотности теплопроводность газа стремится к нулю. Эффузия Если разделить ультраразреженный газ в сосуде на две половины перегородкой с отверстием, то, если размер отверстия будет меньше длины свободного пробега, молекулы будут проходить через отверстие по одиночке. Не сталкиваясь друг с другом. Такой процесс истечения газа называется эффузией. В случае тепловой эффузии, когда стенки обеих частей сосуда находятся при различных температурах T 1 и T 2, условием равновесия будет равенство числа молекул проходящих в единицу времени из одной части сосуда в другую. Следовательно, можно записать : Если имеется смесь двух ультраразреженных газов при одной и той же температуре, то через малое отверстие в первую очередь будут проходить более подвижные, т.е. более легкие молекулы. Такое явление называется изотермической эффузией. Изотермическая эффузия используется, например, при разделении изотопов (легких и тяжелых) молекул одного и того же газа.
14. Распределение Больцмана. Распределение Максвелла - Больцмана. Распределение Гиббса. Барометрическая формула Для изменения давления с высотой, при постоянной температуре, можно получить следующее выражение, называемое барометрической формулой, применяется для исследования как классических, так и квантовых систем. 15.Барометрическая формула.Экспериментальное подтверждение распределения Больцмана. Атмосфера планет. Потенциальная энергия частицы массы т в поле тяготения шарообразного небесного тела равна
где М — масса тела, г — расстояние от центра тела до частицы, G — гравитационная постоянная. Атмосфера планет, в том числе и Земли, не находится в равновесном состоянии. Например, вследствие того что атмосфера Земли находится в неравновесном состоянии, ее температура не постоянна, как это должно было бы быть, а изменяется с высотой (уменьшается с увеличением высоты). Поскольку в конечном счете все системы стремятся к равновесному состоянию, то атмосфера планет постепенно рассеивается. У некоторых из небесных тел, например у Луны, атмосфера полностью исчезла, другие, например Марс, имеют очень разреженную атмосферу. Таким образом, атмосфера Луны уже достигла равновесного состояния, а атмосфера Марса уже находится близко к достижению равновесного состояния. У Венеры атмосфера очень плотная и, следовательно, находится в начале пути к равновесному состоянию. Для количественного рассмотрения вопроса о потере атмосферы планетами необходимо принять во внимание распределение молекул по скоростям. Силу земного притяжения могут преодолеть лишь молекулы, скорость которых превосходит вторую космическую. Эти молекулы находятся в «хвосте» распределения Максвелла и их относительное число незначительно. Тем не менее за значительные промежутки времени потеря молекул является чувствительной. Поскольку вторая космическая скорость у тяжелых планет больше, чем у легких, интенсивность потери атмосферы у массивных небесных тел меньше, чем у легких, т. е. легкие планеты теряют атмосферу быстрее, чем тяжелые. Время потери атмосферы зависит также от радиуса планеты, температуры, состава атмосферы и т. д. Экспериментальная проверка распределения Больцмана. Опыт перрена При выводе распределения Больцмана не налагалось никаких ограничений на массу частиц. Поэтому в принципе оно применимо и для тяжелых частиц. Возьмем в качестве этих частиц, например, песчинки. Ясно, что они расположатся в некотором слое у дна сосуда. Строго говоря, это является следствием распределения Больцмана. При больших массах частиц показатель экспоненты столь быстро изменяется с высотой, что равен нулю везде за пределами слоя песка. Что касается пространства внутри слоя, то там надо принять во внимание объем песчинок. Для того чтобы тяжелые частицы не «осели на дно», а распределились в достаточно большом слое по высоте, необходимо, чтобы их потенциальная энергия была достаточно малой. Этого можно достигнуть, помещая частицы в жидкость, плотность которой лишь на немного меньше плотности материала частиц. Обозначив плотность и объем частиц р и t, а плотность жидкости — р0, видим, что сила, действующая на частицу, равна t (р — р0) g. Следовательно, потенциальная энергия такой частицы на высоте h от дна сосуда равна
Поэтому распределение концентрации этих частиц по высоте дается формулой
Чтобы эффект был достаточно хорошо заметен, частицы должны быть достаточно малыми. Число таких частиц на разных высотах в сосуде считают с помощью микроскопа Барометрическая форму л а. Поскольку формулой давление однозначно выражается через температуру, то распределение Больцмана
позволяет сразу, без дополнительных вычислений написать распределение давлений при тех же условиях, при которых справедлива эта формула, т. е. в условиях равновесия (T= const). Поэтому в случае изотермической атмосферы распределение давления с высотой h дается для каждой компоненты формулами.
Воздух в основном состоит из кислорода и азота. Поэтому формула для изменения давления в нем с высотой имеет вид
близки друг к другу и это изменение несущественно. Упомянуто же здесь лишь для теоретической полноты картины. Фактически смесь газов в отношении давления можно рассматривать как один газ со средней массой молекул
Учитывая, что [m/(kТ)] = ро(r o)/ро-> гДе Ро(ro) и Ро являются плотностью и давлением при h = 0, можно барометрическую формулу записать- в виде.
причем у поверхности Земли принимается р0 = 101,325 кПа. При этом считается, что температура с высотой не изменяется. Если выражать высоту в километрах, то барометрическую формулу удобно также представить в виде (принимая в формуле температуру равной 0°С)
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.255.161 (0.01 с.) |



 где η 0 – постоянная определяемая свойствами жидкости; u – глубина «потенциальной ямы», в которой находится каждая молекула жидкости».
где η 0 – постоянная определяемая свойствами жидкости; u – глубина «потенциальной ямы», в которой находится каждая молекула жидкости».
 -называется коэффициентом
-называется коэффициентом
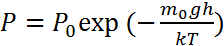 , где m0 – масса молекулы; h – высота. С учетом того, что
, где m0 – масса молекулы; h – высота. С учетом того, что  получим
получим  , Барометрическая формула является частным случаем общего распределения, называемого распределением Больцмана. В самом деле, учитывая, что потенциальная энергия молекулы на высоте h
, Барометрическая формула является частным случаем общего распределения, называемого распределением Больцмана. В самом деле, учитывая, что потенциальная энергия молекулы на высоте h 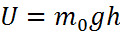 и
и  , получим
, получим  , - распределение Больцмана. Данное распределение справедливо не только для гравитационного поля, но и для любого другого однородного (и не только) поля сил. Если на идеальный газ действует потенциальное поле (например, сила тяжести), то распределение Максвелла должно быть изменено с учетом распределения Больцмана. Подставляя распределение Больцмана в распределение Максвелла, получим
, - распределение Больцмана. Данное распределение справедливо не только для гравитационного поля, но и для любого другого однородного (и не только) поля сил. Если на идеальный газ действует потенциальное поле (например, сила тяжести), то распределение Максвелла должно быть изменено с учетом распределения Больцмана. Подставляя распределение Больцмана в распределение Максвелла, получим  - распределение Максвелла-Больцмана. Распределение Максвелла-Больцмана является частным случаем общего распределения, называемого распределением Гиббса (полученного в 1901 г.):
- распределение Максвелла-Больцмана. Распределение Максвелла-Больцмана является частным случаем общего распределения, называемого распределением Гиббса (полученного в 1901 г.): 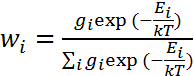 где gi – статистический вес (кратность вырождения (повторения)) рассматриваемого состояния i системы, имеющей энергию Ei. Распределение Гиббса широко
где gi – статистический вес (кратность вырождения (повторения)) рассматриваемого состояния i системы, имеющей энергию Ei. Распределение Гиббса широко
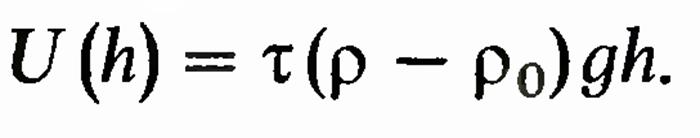


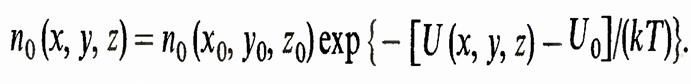
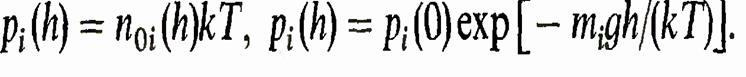
 Однако массы молекул азота и кислорода
Однако массы молекул азота и кислорода





