
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Явление теплопроводности и вязкостиСодержание книги
Поиск на нашем сайте Явление теплопроводности вещества определяет многие очень важные технические процессы и широко применяется в разнообразных расчетах. Эмпирическое уравнение теплопроводности было получено французским ученым Фурье: количество тепла DQ, проходящее за время Dt через площадку S, перпендикулярную к направлению переноса тепла, равно DQ = -c∙(dT/dz) S∙Dt, (9.31) где dT/dz - градиент температуры, dT - изменение температуры на расстоянии dz вдоль направления потока тепла, c - коэффициент теплопроводности вещества. Градиент температуры показывает скорость изменения температуры вдоль потока тепла. Если численно положить (dT/dz)= - 1, S = 1, Dt = = 1, тосогласно (9.31) получим DQ = c. Отсюда следует физический смысл коэффициента c: коэффициент теплопроводности численно равен количеству тепла, проходящего за единицу времени через единичную площадку, расположенную перпендикулярно к потоку тепла, при градиенте температуры, равном единице. Мы рассмотрели два явления переноса: диффузию и теплопроводность. В явлении диффузии наблюдается перенос молекул из одного места пространства в другое, вызванный тепловым движением. В явлении теплопроводности тепловое движение молекул переносит молекулы с большей кинетической энергией в места с меньшей энергией молекул. За счет этого происходит поток тепла. Существует еще одно явление переноса, называемое явлением вязкости и связанное с переносом импульса, которым обладает слой частиц. Это явление было подробно рассмотрено в подразд. 5.3. Для газов вязкость объясняется тем, что при тепловом движении молекулы, перелетая из слоя в слой, переносят импульс слоя. Попадая в слой, движущийся с большей скоростью из более медленного слоя, молекулы замедляют его движение, и наоборот, попадая в слой, движущийся с меньшей скоростью из слоя с более высокой скоростью, молекулы ускоряют его движение. Возникает выравнивание скоростей слоев и, следовательно, сила вязкости. Уравнение вязкости определяется соотношением (5.8). Это уравнение и уравнение теплопроводности (9.31) можно получить, исходя из молекулярно-кинетических представлений. При этом, как и для явления диффузии, применительно к газам получаются следующие теоретические выражения для коэффициентов вязкости и теплопроводности: h = где r - плотность газа; c v - удельная теплоемкость газа при постоянном объеме (будет рассмотрена в подразделе 10.4). Произведение rl не зависит от давления. Следовательно, из формул (9.32) следует, что коэффициенты h и c не зависят от давления, что подтверждается опытом. Однако в области вакуума рассмотренный механизм явления не применим и c ~ p, с уменьшением давления коэффициент теплопроводности уменьшается. В термосах и сосудах Дьюара делают двойные зеркальные стенки и из пространства между ними откачивают воздух до глубокого вакуума. При этом разреженный воздух становится хорошим теплоизолятором.
Термодинамика Термодинамика изучает физические явления с точки зрения тех превращений энергии, которыми эти явления сопровождаются. Первоначально термодинамика возникла как наука о взаимном превращении теплоты в работу. Однако законы, лежащие в основе термодинамики, имеют настолько общий характер, что с большим успехом применяются для исследования различных физических и химических процессов. Термодинамика не вдается в рассмотрение микроскопической картины явлений. Она рассматривает явления, опираясь на основные законы, которые являются обобщением огромного количества опытных данных. Основу термодинамики образуют ее начала. Первое начало устанавливает количественные соотношения, имеющие место при превращениях энергии из одних видов в другие. Второе начало определяет условия, при которых возможны эти превращения, т.е. определяет возможные направления процессов.
|
|||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.01 с.) |

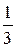 r vсрl и c =
r vсрl и c = 


