
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графическое изображение гармонических колебаний. Векторная диаграмма.Содержание книги
Поиск на нашем сайте
Сложение нескольких колебаний одинакового направления (или, что то же самое, сложение нескольких гармонических функций) значительно облегчается и становится наглядным, если изображать колебания графически в виде векторов на плоскости.
w0t1+a; w0t2+a; w0t3+a; и т.д. А проекция этого вектора будет перемещаться по оси «x» в пределах от –А до +А. Причем координата этой проекции будет изменяться со временем по закону:
Следовательно, проекция конца вектора на некоторую произвольную ось будет совершать гармоническое колебание с амплитудой равной длине вектора, круговой частотой равной угловой скорости вращения вектора и начальной фазой равной углу, образованному вектором с осью в начальный момент времени. Итак, гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью “x” угол равный начальной фазе колебания.
Представим оба колебания с помощью векторов
Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения векторов. Этот способ отличается большей простотой и наглядностью, чем использование тригонометрических преобразований. Проанализируем выражение для амплитуды. Если разность фаз обоих колебаний a2 - a1 = 0, то амплитуда результирующего колебания равна сумме (а 2 + а 1). Если разность фаз a2 - a1 = +p или -p, т.е. колебания находятся в противофазе, то амплитуда результирующего колебания равна Если частоты колебаний x1 и x2 неодинаковы, векторы
|
||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.155 (0.006 с.) |

 Возьмем ось, которую обозначим “x”. Из точки О, взятой на оси, под углом a, равным начальной фазе колебаний, отложим вектор длины A (рис. 8.3). Спроектируем вектор A на ось x, получим x0=A cos a – начальное смещение колеблющейся точки от положения равновесия. Приведем этот вектор во вращение против часовой стрелки с угловой скоростью w0. Положение этого вектора в любые моменты времени будет характеризоваться углами, равными:
Возьмем ось, которую обозначим “x”. Из точки О, взятой на оси, под углом a, равным начальной фазе колебаний, отложим вектор длины A (рис. 8.3). Спроектируем вектор A на ось x, получим x0=A cos a – начальное смещение колеблющейся точки от положения равновесия. Приведем этот вектор во вращение против часовой стрелки с угловой скоростью w0. Положение этого вектора в любые моменты времени будет характеризоваться углами, равными: .
. Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты. Смещение колеблющегося тела “x” будет суммой смещений x1 и x2, которые запишутся следующим образом:
Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты. Смещение колеблющегося тела “x” будет суммой смещений x1 и x2, которые запишутся следующим образом:

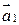 и
и  (рис. 8.4) По правилам сложения векторов строим результирующий вектор
(рис. 8.4) По правилам сложения векторов строим результирующий вектор 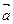 . Проекция этого вектора на ось X будет равна сумме проекций слагаемых векторов: x=x1+x2. Следовательно, вектор
. Проекция этого вектора на ось X будет равна сумме проекций слагаемых векторов: x=x1+x2. Следовательно, вектор  представляет собой результирующее колебание. Этот вектор вращается с той угловой скоростью w0, что и векторы
представляет собой результирующее колебание. Этот вектор вращается с той угловой скоростью w0, что и векторы  и
и  .
.
 .
.


