
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Путь при неравномерном движении.Содержание книги
Поиск на нашем сайте
Если v(t) = const, то движение равномерное, v(t) ¹ const – то движение неравномерное. 2.5. Ускорение. Ускорение при равнопеременном и неравнопеременном прямолинейном движении. При неравномерном движении необходимо знать закономерность, по которой скорость изменяется со временем. Для этого вводится величина, характеризующая быстроту изменения скорости со временем и называемая ускорением «
Среднее ускорение направлено также как приращение скорости, т.е. под углом к траектории в сторону ее вогнутости. В общем случае величина среднего ускорения может быть различной на различных участках траектории и зависеть от величины промежутка времени Dt, по которому проводится усреднение. В пределе при Dt ® 0 точка В будет стремиться к точке А и среднее ускорение по пути АВ превратится в мгновенное или истинное ускорение Поэтому Итак, мгновенное ускорение движения в любой точке траектории есть вектор, направленный под углом к траектории в сторону ее вогнутости, а по величине равный пределу среднего ускорения при стремлении промежутка времени к нулю. Из выше приведенных формул следует, что ускорение измеряется в м/с2; [а] = м/с2. По модулю величина ускорения равна Если рассматривать движение тела в пространстве, то вектор ускорения
Замечание: Следует помнить, что ускорение характеризует не только изменение модуля скорости, но и изменение направления вектора скорости. Например, равномерное движение по окружности является ускоренным из-за изменения направления вектора скорости с течением времени, хотя модуль скорости остается неизменным. Рассмотрим частный случай ускоренного движения. Прямолинейное движение с постоянным ускорением называется равноускоренным (a = const). В этом случае мгновенное ускорение будет равно среднему ускорению за любой промежуток времени. И тогда
1. Если а > 0, то движение равноускоренное. Из (2.3) следует, что v=v0+ a (t - t0) и при t0 = 0 v=v0+ a t при a > 0 скорость v возрастает. Направления 2. Если a < 0, то движение равнозамедленное и скорость v уменьшается. Зная зависимость v от t можно подсчитать путь, пройденный телом при равнопеременном движении (рис. 2.10). Имеем v=v0 + at, домножим на dt. dS = v·dt = v0·dt + a·t·dt. Интегрируем слева от 0 до S, справа от 0 до t. Получаем, что
Тогда
Данная формула верна, если за время движения знаки начальной скорости и ускорения совпадают. Наклон прямой v0+at на рисунке 2.10 зависит от величины «а», чем «а» больше, тем больше угол наклона. «S» численно рано площади заштрихованной фигуры.
Криволинейное движение.
|
|||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.007 с.) |

 За малый промежуток времени Dt перемещение графически изображается в виде прямоугольника, высота которого равна некоторому значению средней скорости v (рис.2.8). Тогда для любого промежутка времени от 0 до t суммируют все эти элементарные площадки SDS, т.е. графически эта сумма представляет собой площадь фигуры ABCD (Svср.×Dt). Чаще всего площадь фигуры дает нам также путь, пройденный при неравномерном движении (математически это записывается как предел).
За малый промежуток времени Dt перемещение графически изображается в виде прямоугольника, высота которого равна некоторому значению средней скорости v (рис.2.8). Тогда для любого промежутка времени от 0 до t суммируют все эти элементарные площадки SDS, т.е. графически эта сумма представляет собой площадь фигуры ABCD (Svср.×Dt). Чаще всего площадь фигуры дает нам также путь, пройденный при неравномерном движении (математически это записывается как предел).
 .
. ».
». Пусть материальная точка переместилась за малый промежуток времени Dt из точки А, где она имела скорость
Пусть материальная точка переместилась за малый промежуток времени Dt из точки А, где она имела скорость 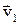 в точку В, где скорость
в точку В, где скорость  (рис.2.9). Приращение скорости точки есть вектор
(рис.2.9). Приращение скорости точки есть вектор  , равный разности конечной и начальной скоростей:
, равный разности конечной и начальной скоростей:  .
. Отношение изменения скорости к промежутку времени, за который это изменение произошло, называется средним ускорением
Отношение изменения скорости к промежутку времени, за который это изменение произошло, называется средним ускорением 
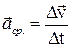 . Это понятие
. Это понятие  . (2.2)
. (2.2) . Т.е. величина ускорения определяется первой производной скорости v по времени или второй производной пути по времени.
. Т.е. величина ускорения определяется первой производной скорости v по времени или второй производной пути по времени. можно представить через его проекции на оси X, Y, Z, аналогично как это делали для вектора
можно представить через его проекции на оси X, Y, Z, аналогично как это делали для вектора  .
.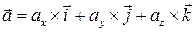 ;
;
 ; (2.3)
; (2.3) В зависимости от поведения скорости со временем различают равноускоренное и «равнозамедленное» движения. Кавычки поставлены, чтобы подчеркнуть, что в любом случае движение происходит с постоянным ускорением.
В зависимости от поведения скорости со временем различают равноускоренное и «равнозамедленное» движения. Кавычки поставлены, чтобы подчеркнуть, что в любом случае движение происходит с постоянным ускорением. .
. . (2.4)
. (2.4)


