
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое толкование второго начала термодинамикиСодержание книги
Поиск на нашем сайте Состояние макроскопического тела (т.е. тела, образованного огромным числом молекул) может быть задано с помощью объема, давления и температуры. Данное макроскопическое состояние газа с определенными средними значениями параметров представляет собой непрерывную Так как система стремится к равномерному распределению молекул по объему, то согласно рассмотренному примеру она должна стремиться к максимуму термодинамической вероятности. С другой стороны, энтропия системы тоже стремится к максимальному значению. Следовательно, существует связь между энтропией и термодинамической вероятностью, теоретически полученная Больцманом: S = k ln W, (10.28) где k - постоянная Больцмана. Второе начало термодинамики приобретает следующий статистический смысл: изолированная система самопроизвольно может переходить только от состояний менее вероятных к состояниям более вероятным.
Реальные газы Уравнение Ван-дер-Ваальса Поведение реальных газов при их малых плотностях хорошо описывается уравнением Клапейрона:
где
где Vm - объем моля реального газа. Силы притяжения со стороны других молекул вызывают уменьшение скорости молекулы, соударяющейся со стенкой, поэтому силы взаимодействия молекул уменьшают давление газа на стенки сосуда на величину pi . Давление реального газа запишется в виде p = (p + p i )·(Vm - b) = RT. (11.3) Величина pi зависит от объема газа. Если рассмотреть две половинки малого объема газа, то при увеличении количества молекул в них в n раз сила их взаимодействия f увеличится в n2 раз (рис. 11.1). Следовательно, величина pi ~ r 2, где r - плотность газа. Учитывая, что при неизменной массе газа величина r обратно пропорциональна объему V, получим pi = a / (p + a /
Итак, уравнение Ван-дер-Ваальса позволило предсказать наличие неустойчивых состояний и неплохо количественно описать переход вещества из газообразного состояния в жидкое.
|
|||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 746; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.01 с.) |

 смену близких микроскопических состояний, отличающихся друг от друга распределением одних и тех же молекул в разных частях объема и распределением импульса между различными молекулами. Для примера рассмотрим распределение только четырех молекул по двум половинкам объема (рис.10.11). Первое макро-состояние, при котором в левой части объема находятся все молекулы, реализуется одним микросостоянием. Термодинамической вероятностью или статистическим весом W называют число микросостояний, с помощью которого реализуется данное макро-состояние. Первое макро-состояние имеет термодинамическую вероятность W= 1. Второе макро-состояние, при котором в левой части объема находятся три молекулы, а в правой - одна, реализуется четырьмя способами (в правой части можно по очереди разместить четыре различных молекулы), и его термодинамическая вероятность W = 4. Третье макро-состояние, при котором молекулы поровну распределены по половинкам объема, имеет термодинамическую вероятность W = 6. Точное определение того, что подразумевается под ”числом микроскопических способов осуществления” теплового состояния тела, дается в курсе статистической физики.
смену близких микроскопических состояний, отличающихся друг от друга распределением одних и тех же молекул в разных частях объема и распределением импульса между различными молекулами. Для примера рассмотрим распределение только четырех молекул по двум половинкам объема (рис.10.11). Первое макро-состояние, при котором в левой части объема находятся все молекулы, реализуется одним микросостоянием. Термодинамической вероятностью или статистическим весом W называют число микросостояний, с помощью которого реализуется данное макро-состояние. Первое макро-состояние имеет термодинамическую вероятность W= 1. Второе макро-состояние, при котором в левой части объема находятся три молекулы, а в правой - одна, реализуется четырьмя способами (в правой части можно по очереди разместить четыре различных молекулы), и его термодинамическая вероятность W = 4. Третье макро-состояние, при котором молекулы поровну распределены по половинкам объема, имеет термодинамическую вероятность W = 6. Точное определение того, что подразумевается под ”числом микроскопических способов осуществления” теплового состояния тела, дается в курсе статистической физики.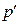
 = RT, (11.1)
= RT, (11.1) . Выражение (11.3) запишется в виде
. Выражение (11.3) запишется в виде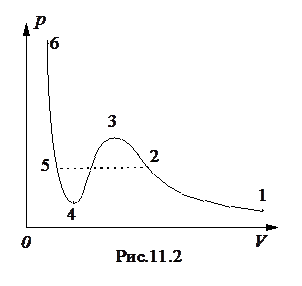 где a - поправка Ван-дер-Ваальса, учитывающая притяжение молекул. Формулу (11.4.) называют уравнением Ван-дер-Ваальса. Это уравнение гораздо лучше согласуется с экспериментом, чем уравнение Клапейрона. Изотерма Ван-дер-Ваальса построена на рис. 11.2. Она отличается от изотермы идеального газа наличием S -образного участка 2-3-4-5, который обычно не реализуется на опыте. Если взять некоторый газ, состояние которого соответствует точке 1, и изотермически сжимать его, то уравнение Ван-дер-Ваальса на участке 1-2 будет хорошо описывать опытную кривую. При дальнейшем сжатии газа экспериментальная кривая пройдет по штриховой линии 2-5. В точке 2 газ является насыщенным паром, и при дальнейшем уменьшении его объема часть пара конденсируется. Система распадается на две фазы: жидкую и газообразную. Давление насыщенного пара является постоянным и линия 2-5 параллельна оси абсцисс. При уменьшении объема системы по линии 2-5 растет количество жидкой фазы, и в точке 5 насыщенный пар полностью конденсируется в жидкость. Жидкость является малосжимаемой, поэтому при дальнейшем уменьшении объема давление быстро возрастает. Участок 5-6 изотермы Ван-дер-Ваальса полностью совпадает с опытной кривой. S‑ образный участок изотермы, представляющий собой область неустойчивых состояний, на опыте обычно на реализуется. Участок 3-4 представляет собой область совершенно неустойчивых состояний и экспериментально его невозможно реализовать. При некоторых условиях, например, отсутствии центров конденсации или кипения, можно реализовать участки 2-3 и 4-5. Участок 2-3 соответствует перегретому пару, а участок 4-5 - перегретой или растянутой жидкости. Эти вполне устойчивые состояния называются метастабильными, и если искусственно ввести в метастабильную систему центры конденсации, то система скачком перейдет в двухфазное состояние. Воду можно перегреть на несколько десятков градусов, и если насыпать в нее немного мелкого песка, то происходит вскипание со взрывом. При перегонке многих жидкостей с целью очистки во избежание перегрева необходимо вводить специальные предметы в качестве центров кипения. Метастабильные состояния жидкости и пара широко используются при регистрации элементарных частиц.
где a - поправка Ван-дер-Ваальса, учитывающая притяжение молекул. Формулу (11.4.) называют уравнением Ван-дер-Ваальса. Это уравнение гораздо лучше согласуется с экспериментом, чем уравнение Клапейрона. Изотерма Ван-дер-Ваальса построена на рис. 11.2. Она отличается от изотермы идеального газа наличием S -образного участка 2-3-4-5, который обычно не реализуется на опыте. Если взять некоторый газ, состояние которого соответствует точке 1, и изотермически сжимать его, то уравнение Ван-дер-Ваальса на участке 1-2 будет хорошо описывать опытную кривую. При дальнейшем сжатии газа экспериментальная кривая пройдет по штриховой линии 2-5. В точке 2 газ является насыщенным паром, и при дальнейшем уменьшении его объема часть пара конденсируется. Система распадается на две фазы: жидкую и газообразную. Давление насыщенного пара является постоянным и линия 2-5 параллельна оси абсцисс. При уменьшении объема системы по линии 2-5 растет количество жидкой фазы, и в точке 5 насыщенный пар полностью конденсируется в жидкость. Жидкость является малосжимаемой, поэтому при дальнейшем уменьшении объема давление быстро возрастает. Участок 5-6 изотермы Ван-дер-Ваальса полностью совпадает с опытной кривой. S‑ образный участок изотермы, представляющий собой область неустойчивых состояний, на опыте обычно на реализуется. Участок 3-4 представляет собой область совершенно неустойчивых состояний и экспериментально его невозможно реализовать. При некоторых условиях, например, отсутствии центров конденсации или кипения, можно реализовать участки 2-3 и 4-5. Участок 2-3 соответствует перегретому пару, а участок 4-5 - перегретой или растянутой жидкости. Эти вполне устойчивые состояния называются метастабильными, и если искусственно ввести в метастабильную систему центры конденсации, то система скачком перейдет в двухфазное состояние. Воду можно перегреть на несколько десятков градусов, и если насыпать в нее немного мелкого песка, то происходит вскипание со взрывом. При перегонке многих жидкостей с целью очистки во избежание перегрева необходимо вводить специальные предметы в качестве центров кипения. Метастабильные состояния жидкости и пара широко используются при регистрации элементарных частиц.


