
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальная энергия упруго деформированного тела.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруго деформированное тело (например, сжатая пружина, растянутый стержень и т.п.). В этом случае потенциальная энергия зависит от взаимного расположения отдельных частей тела (например, от расстояния между соседними витками пружины). Определим работу, которую необходимо затратить для растяжения (или сжатия) пружины на величину «x» (рис.3.8). Будем считать, что пружина подчиняется закону Гука, т.е. упругая сила пропорциональна деформации. Будем проводить растяжение пружины очень медленно, чтобы силу
Пусть под действием силы Отсюда
Эта работа идет на увеличение потенциальной энергии пружины. В предположении, что потенциальная энергия недеформированной пружины равна «0» (U 1 = 0) получаем
– потенциальная энергия упругой деформации пружины.
Закон сохранения энергии. Без нарушения общности рассмотрим систему, состоящую из двух частиц массами m1 и m2. Пусть частицы взаимодействуют друг с другом с силами
Умножим каждое уравнение на
1. Распишем первый член в правой части. Работа внутренних сил равна Тогда
Учитывая, что силы Следовательно, Скалярное произведение Выражение
Функция Работа внутренних сил будет равна
т.е. не зависит от пути, по которому перемещаются частицы, а определяется начальной и конечной конфигурациями системы. Т.е. силы взаимодействия вида Итак, работа внутренних сил равна убыли потенциальной энергии взаимодействия
2. Второй член представляет работу внешних сил и равен убыли потенциальной энергии системы во внешнем поле консервативных сил
3. Последний член представляет работу неконсервативных внешних сил После этих замечаний можно записать
Величина T + Uвз. + Uвн. = E (3.13) – называется полной механической энергией системы. Если внешние неконсервативные силы отсутствуют, т.е. Е=const – закон сохранения механической энергии. ОПРЕДЕЛЕНИЕ: полная механическая энергия системы тел, на которые действуют лишь консервативные силы, остается постоянной. Для замкнутой системы, т.е. системы, на тела которой не действуют никакие внешние силы, закон сохранения примет вид: E = T + Uвз. = const Если в замкнутой системе, кроме консервативных сил действуют неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется. Рассматривая консервативные силы как внешние, получим
или после интегрирования
Анализ закона сохранения показывает, что полная энергия, оставаясь в консервативной системе величиной постоянной, может переходить из одних видов в другие. При действии неконсервативных сил возможен переход механической энергии в другие немеханические виды энергии. В этом случае справедлив более общий закон сохранения: ОПРЕДЕЛЕНИЕ: в изолированной от любых внешних воздействий системе остается постоянной сумма всех видов энергии (включая и немеханические). К этому добавим, что в природе и технике постоянно имеют место превращения энергии из одних видов в другие. Проиллюстрируем это таблицей.
Для графического изображения закона сохранения энергии рассмотрим случай, когда тело бросаем вверх. Если не учитывать силу сопротивления воздуха Fсопр., то систему «тело-Земля» можно рассматривать, как изолированную и консервативную, для которой E = Eк. + Up. = const Из графика (рис. 3.10) видно, что по мере поднятия тела над поверхностью Земли его потенциальная энергия возрастает от величины Up(h1) до Up(h2), но одновременно с этим точно на такую же величину уменьшается кинетическая энергия системы Eк., а полная энергия тела остается величиной постоянной, что соответствует линии BA || h. Очевидно: 1. При h=0 имеем Up=0, а E=Eк., что соответствует линии ОВ; 2. При h = max имеем Up = max (Eк. = 0), а E = Up, что соответствует линии AC. САМОСТОЯТЕЛЬНО: Упругий и неупругий центральный удар шаров; Условия равновесия механической системы. Механика твердого тела.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 973; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.011 с.) |

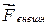 , с которой мы действуем на пружину, можно было все время считать равной по величине упругой силе
, с которой мы действуем на пружину, можно было все время считать равной по величине упругой силе 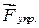 . Далее будем считать, что сила действует в направлении перемещения, т.е.
. Далее будем считать, что сила действует в направлении перемещения, т.е. 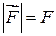 .
.
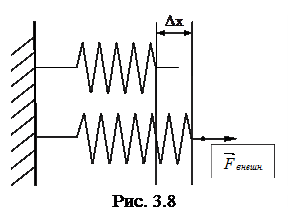 Исходя из предыдущего, можно записать Fвнешн. = -Fупр. = kx, где x – удлинение пружины, k – коэффициент жесткости пружины, а согласно закону Гука направление упругой силы и перемещения противоположны (силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) и имеют, в конечном счете, электрическую природу).
Исходя из предыдущего, можно записать Fвнешн. = -Fупр. = kx, где x – удлинение пружины, k – коэффициент жесткости пружины, а согласно закону Гука направление упругой силы и перемещения противоположны (силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) и имеют, в конечном счете, электрическую природу).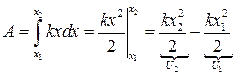 ;
;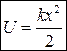 (3.12)
(3.12) и
и 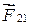 , модули которых зависят от расстояния R12 между частицами. Установлено, что такие силы являются консервативными, т.е. работа, совершаемая такими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть также, кроме внутренних сил на первую частицу действует внешняя консервативная сила
, модули которых зависят от расстояния R12 между частицами. Установлено, что такие силы являются консервативными, т.е. работа, совершаемая такими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть также, кроме внутренних сил на первую частицу действует внешняя консервативная сила 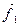 и внешняя неконсервативная сила
и внешняя неконсервативная сила  . Аналогично для второй частицы. Тогда уравнения движения частиц можно записать в виде:
. Аналогично для второй частицы. Тогда уравнения движения частиц можно записать в виде:
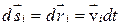 и сложим полученные выражения.
и сложим полученные выражения.
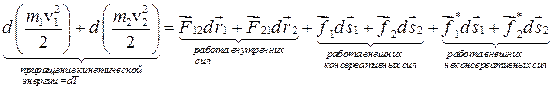
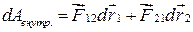 . Для замкнутой системы
. Для замкнутой системы  , а
, а 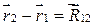 , где
, где  и
и  – радиус-векторы частиц.
– радиус-векторы частиц. .
. , где f(R 12 ) – некоторая функция R 12,
, где f(R 12 ) – некоторая функция R 12, 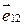 – орт вектора
– орт вектора 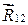 .
. .
.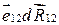 равно приращению dR 12 расстояния между частицами, тогда
равно приращению dR 12 расстояния между частицами, тогда 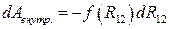 .
.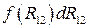 есть приращение некоторой функции
есть приращение некоторой функции 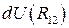 . Следовательно,
. Следовательно,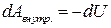 .
.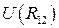 представляет потенциальную энергию взаимодействия.
представляет потенциальную энергию взаимодействия.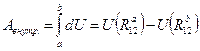 ,
, являются консервативными.
являются консервативными.
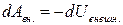
 .
.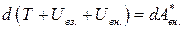
 , то
, то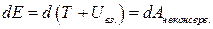
 .
.
 В таблице не отражено, что при любом превращении часть энергии превращается в теплоту.
В таблице не отражено, что при любом превращении часть энергии превращается в теплоту.


