
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Импульс. Закон сохранения импульса.Содержание книги
Поиск на нашем сайте В механической системе, состоящей из нескольких тел, существуют как силы взаимодействия между телами системы, которые называются внутренними, так и силы взаимодействия этих тел с телами, не входящими в данную систему, которые называются внешними. Если внешние силы отсутствуют, то механическая система называется замкнутой. Для замкнутой механической системы существует несколько физических величин, которые остаются постоянными с течением времени. Одной из таких величин является импульс тела, который является вектором и равен произведению массы тела m на вектор скорости тела v: p = m v. Для механической системы ее импульс равен векторной сумме импульсов, составляющих ее n тел:
Пользуясь выражением для импульса и учитывая постоянство массы тела, представим второй закон Ньютона в следующем виде:
Рассмотрим изолированную систему, состоящую из двух движущихся тел. Сталкиваясь друг с другом, тела (упругие шары) будут изменять свой импульс. Рассматривая взаимодействие тел в течение небольшого промежутка времени Dt и применяя к каждому телу закон изменения импульса, можно записать:
Складывая равенства почленно, получим:
Тогда
Это означает, что сумма импульсов обеих тел системы не изменяется со временем, т.е. Введем величину Тогда для системы из “n” тел
или из II закона Ньютона
т.к. система замкнута. Эти равенства выражают закон сохранения импульса. ОПРЕДЕЛЕНИЕ: Полный вектор импульса замкнутой (или изолированной) системы тел с течением времени не изменяется. Пусть теперь на тела A и B действуют теперь как внутренние, так и внешние силы: на тело A – Тогда
или, что равносильно для системы из “n” тел: Складывая эти уравнения с учетом, что
Следовательно, производная по времени от вектора импульса системы равна сумме всех внешних сил, приложенных к телам системы. Для замкнутой системы ОПРЕДЕЛЕНИЕ: Импульс замкнутой системы тел остается постоянным. Отметим, что импульс системы тел остается постоянным и для системы, подверженной внешним воздействиям, при условии, что внешние силы, действующие на тела системы, в сумме дают нуль. Если даже сумма внешних сил не равна нулю, но проекция этой суммы на некоторое направление есть нуль, то составляющая импульса в этом направлении будет постоянной. Работа и энергия. Пусть тело, на которое действует сила ОПРЕДЕЛЕНИЕ: Работой называется скалярная величина, численно равная произведению действующей силы (FS) на направление перемещения и величины пути (S), проходимого точкой приложения силы A=FS×S.
Работа алгебраическая величина. Если 1. 2. 3. Последнее обстоятельство особенно отчетливо показывает, что понятие работы в механике существенно отличается от обыденного представления о работе. Пример: Чтобы держать тяжелый груз, а тем более нести его по горизонтальному пути, носильщик затрачивает много усилий, хотя якобы «не совершает работу». Работа как механическая величина в этих случаях не равна нулю, так как эта работа складывается из множества перемещений вниз и вверх. Причем при перемещении вниз уменьшение потенциальной энергии в поле тяжести не переходит в полезную работу.
Тогда для элементарного участка пути: DA @ FS×DS. А работа на всем пути S будет вычисляться как сумма элементарных работ: При ×DS i ® 0 получим строгое равенство:
График FS как функции положения точки на траектории представлен на рис. 3.3. Видно, что элементарная работа равна площади заштрихованной полоски, а работа A на пути от точки 1 до точки 2 численно равна площади фигуры, ограниченной кривой FS, вертикальными прямыми 1 и 2 и осью S. Воспользовавшись скалярным произведением векторов, выражение для работы можно записать в виде:
где под
где В системе СИ единицей работы является 1Дж, который равен работе, совершаемой силой в 1Н на пути в 1м. 1Дж=1Н×1м.
Мощность. На практике имеет значение не только величина совершенной работы, но и время, в течение которого она совершается. Из всех механизмов наиболее выгодными являются те, которые за меньшее время выполняют большую работу. Поэтому для характеристики механизмов, предназначенных для совершения работы, вводится величина, показывающая, какую работу данный механизм совершает в единицу времени. Эта величина называется мощностью. ОПРЕДЕЛЕНИЕ: Мощность – физическая величина, численно равная работе, совершаемой телом за единицу времени. Определяется мощность, как отношение работы DA к промежутку времени Dt, за который она совершается Если за время dt под действием силы произошло перемещение тела на Тогда мощность
Следовательно, мощность оказывается равной скалярному произведению силы на вектор скорости, с которой движется точка приложения силы: W=F×v×cosa, где a – угол между направлением силы и скорости. а) a=0, поэтому cos a=1, следовательно, W=Fv – max; б) В системе СИ единицей мощности является 1Вт. Это мощность, при которой в единицу времени (1с) совершается работа в 1Дж. Энергия. Из опыта известно, что тела часто оказываются в состоянии совершать работу над другими телами. ОПРЕДЕЛЕНИЕ: Физическая величина, характеризующая способность тела или системы тел совершать работу, называется энергией. Пример: 1) Катящийся шар обладает энергией, т.к., сталкиваясь с другим телом, перемещает его, т.е. совершает работу. 2) Растянутая пружина также обладает энергией, т.к. после устранения деформирующей силы, совершает работу по перемещению своих частей (витков) или какого-либо другого тела. 3) система, состоящая из Земного шара и расположенного на некоторой высоте тела, обладает энергией, т.к. при устранении связи, удерживающей тело на высоте, это тело начнет двигаться и может совершить работу. Итак, названные тела обладают энергией независимо от того, совершают они в данный момент времени работу или нет. Энергия характеризует способность системы к совершению работы при переходе из одного состояния в другое. Если в первом состоянии энергия системы Е1, а во втором Е2, то А = Е2 - Е1. Если работа внешних сил A > 0, то энергия системы возрастает Е2 ‑ Е1 > 0. Если A<0 (система совершает работу), то энергия системы убывает. Е2-Е1<0, т.е. убыль энергии в этом случае численно равна работе против тех сил, которые препятствуют движению тела. Следовательно, система может совершать работу только за счет изменения своей энергии. Энергия тела может быть обусловлена двумя причинами: 1. Во-первых, движением тела с некоторой скоростью v. Энергия этого вида называется кинетической энергией (от греческого «кинетикос» – относящийся к движению). 2. Во-вторых, взаимным расположением тел или частей тела и характером их взаимодействия (или более, строго говоря, нахождением тела в потенциальном поле сил). Энергия этого вида называется потенциальной (от латинского «potential» – возможность). Замечание: Поле сил называется потенциальным, если работа, совершаемая над телом силами, зависящими только от положения тела, не зависит от пути, а определяется только начальным и конечным положением тела в пространстве. А сами силы называются консервативными. Далее рассмотрим введенные понятия более подробно. Кинетическая энергия тела. Рассмотрим простейшую систему, состоящую из одной частицы (материальной точки). Напишем уравнение движения частицы Соответственно,
После этого получаем:
Если система замкнута, то Говорят, что для изолированной системы кинетическая энергия является интегралом движения (т.е. остается неизменной). Если на частицу действует сила
Левая часть этого равенства представляет собой разность значений кинетической энергии в точках 2 и 1, т.е. приращение кинетической энергии на пути 1 – 2. Учтя это, получим:
где А – работа силы на пути 1®2, поэтому иногда пишут вместо А ® А12. Итак: Работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы: А12 = Т2 - Т1. Энергия имеет такую же размерность, как и работа.
|
|||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.007 с.) |


 (3.2)
(3.2)

 ,
,  – результирующие силы, действующие на каждое тело,
– результирующие силы, действующие на каждое тело, ,
,  – скорости в начале и в конце рассматриваемого промежутка времени.
– скорости в начале и в конце рассматриваемого промежутка времени.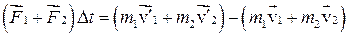
 .
. .
. , представляющую вектор импульса всей системы (или полный импульс системы).
, представляющую вектор импульса всей системы (или полный импульс системы).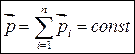 (3.3)
(3.3) , (3.4)
, (3.4) и
и  ,
,
 .
. , получаем
, получаем . (3.5)
. (3.5) , вследствие чего полный импульс не зависит от времени. Это утверждение представляет собой содержание закона сохранения импульса. Повторим его:
, вследствие чего полный импульс не зависит от времени. Это утверждение представляет собой содержание закона сохранения импульса. Повторим его: , проходит, двигаясь по некоторой траектории путь S. При этом сила либо изменяет скорость тела, сообщая ему ускорение, либо компенсирует действие другой силы (или сил), противодействующих движению. Для характеристики действия силы, в результате которого совершается перемещение тела, используется величина, называемая работой.
, проходит, двигаясь по некоторой траектории путь S. При этом сила либо изменяет скорость тела, сообщая ему ускорение, либо компенсирует действие другой силы (или сил), противодействующих движению. Для характеристики действия силы, в результате которого совершается перемещение тела, используется величина, называемая работой. Это выражение справедливо, если величина проекции силы FS=const. В частности, это имеет место, когда тело движется прямолинейно и постоянная по величине сила F образует с направлением движения постоянный угол a (рис. 3.2). Т.к. FS=F· cos a, то A=F·S· cos a.
Это выражение справедливо, если величина проекции силы FS=const. В частности, это имеет место, когда тело движется прямолинейно и постоянная по величине сила F образует с направлением движения постоянный угол a (рис. 3.2). Т.к. FS=F· cos a, то A=F·S· cos a. , то cos a > 0 Þ A > 0;
, то cos a > 0 Þ A > 0; , то A<0, т.к. cos a < 0;
, то A<0, т.к. cos a < 0; , то cos a = 0 Þ A = 0.
, то cos a = 0 Þ A = 0. Если величина проекции силы на направление перемещения не постоянная величина во время движения, то для вычисления работы необходимо путь S разбить на элементарные участки DS, взяв их настолько малыми, что за время прохождения телом такого участка величину FS можно было считать практически неизменной (рис. 3.3).
Если величина проекции силы на направление перемещения не постоянная величина во время движения, то для вычисления работы необходимо путь S разбить на элементарные участки DS, взяв их настолько малыми, что за время прохождения телом такого участка величину FS можно было считать практически неизменной (рис. 3.3). .
.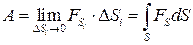
 , (3.6)
, (3.6)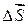 подразумевается вектор элементарного перемещения. Если сила имеет постоянную величину и направление, то вектор
подразумевается вектор элементарного перемещения. Если сила имеет постоянную величину и направление, то вектор  , (3.7)
, (3.7)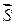 – вектор перемещения, а SF – его проекция на направление силы.
– вектор перемещения, а SF – его проекция на направление силы. ; Если за одинаковые, сколь угодно малые промежутки времени совершается неодинаковая работа, то мощность будет зависеть от времени и в этом случае вводится понятие мгновенной мощности:
; Если за одинаковые, сколь угодно малые промежутки времени совершается неодинаковая работа, то мощность будет зависеть от времени и в этом случае вводится понятие мгновенной мощности:  ;
; , то элементарная работа dA, совершаемая за время dt будет равна
, то элементарная работа dA, совершаемая за время dt будет равна  .
. . (3.8)
. (3.8) , значит W = 0.
, значит W = 0. . Здесь
. Здесь  . Тогда
. Тогда  . Здесь
. Здесь  – есть приращение скорости
– есть приращение скорости  за время dt.
за время dt. .
. (3.9)
(3.9) , следовательно,
, следовательно,  , а сама величина
, а сама величина  . Эта величина называется кинетической энергией частицы.
. Эта величина называется кинетической энергией частицы. .
. ,
,


