
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Максвелловское распределение молекул по скоростямСодержание книги
Поиск на нашем сайте
В результате столкновений молекулы обмениваются скоростями, а в случае тройных и более сложных столкновений молекула может иметь временно очень большие и очень малые скорости. Хаотичное движение приводит к хаотичному распределению молекул по скоростям. Это распределение можно получить, обобщив закон Больцмана. Пусть в элементе объема DxDyDz находится число молекул DN = nDxDyDz, где n - число молекул в единице объема. Подставляя n из формулы (9.15), получим DN = no exp[- Eп /(kT) ] DxDyDz. Как доказывается в статистической физике, распределение Больцмана можно обобщить, построив подобно обычному пространству дополнительное пространство скоростей молекул и рассмотрев его элемент Dvx Dvy Dvz. Получим DN = A exp[-E /(kT)]DxDyDzDvxDvyDvz, (9.16) где E = mv 2 /2 + mgh - полная энергия молекулы; A - постоянная величина; DN - число молекул, находящихся в объеме DxDyDz, скорости которых попадают в интервал Dv x Dv y Dv z. Считая, что в малом объеме DxDyDz энергия mgh постоянна и вводя Dn = DN/(DxDyDz), запишем (9.16) в виде Dn = B exp[-mv2 /(2kT)] DvxDvyDvz, (9.17)
Dn = B exp[-m v2 /(2kT)] 4p v2 Dv. (9.18) Максвелл ввел специальную функцию распределения молекул по скоростям f(v) = Dn/(nDv), которая показывает, какое относительное число молекул имеет скорости в интервале от v до v + Dv. Легко видеть, что å f(v)Dvi» å Dni /n = 1. Переходя к пределу, получим
Данное выражение называют условием нормировки функции распределения. С учетом (9.18) функцию распределения можно записать в виде u2 = mv2/(2kT), (9.20) и запишем функцию распределения в виде f(v) = C exp(-u2) u2. (9.21)
Отсюда видим, что с повышением температуры наиболее вероятная скорость возрастает. Кривая 2 на рис.9.5, соответствующая более высокой температуре, смещена вправо по сравнению с кривой 1. Это означает, что с повышением температуры скорости всех молекул возрастают, но характер распределения остается. Площадь, ограниченная каждой из кривых, в соответствии с условием (9.19) равна единице. Из анализа кривых на рис.9.5 видно, что относительное число молекул, скорости которых малы, невелико. Относительное число молекул, скорости которых намного больше v нв, мало. Однако всегда существует небольшое число молекул с очень большими скоростями движения. Исходя из этого, легко понять сущность процесса испарения, при котором наиболее быстрые (“горячие”) молекулы покидают жидкость, и из-за этого в целом температура ее при испарении понижается. Постоянную C в выражении (9.21) определяют, используя условие нормировки (9.19). Подставляя формулу (9.21) в выражение (9.19), получим C = 4/( С помощью Максвелловского распределения молекул по скоростям можно рассчитать среднюю скорость молекул по формуле v ср = vср = Аналогично рассчитывается средняя квадратичная скорость: vкв2 = Видим, что наибольшее значение имеет средняя квадратичная скорость молекул. Примерно на 10% меньше, чем v кв, средняя скорость и на 20% меньше, чем v кв, наиболее вероятная скорость.
|
||||
|
Последнее изменение этой страницы: 2016-12-11; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.147.12 (0.007 с.) |

 где B - постоянная величина, Dn - число молекул в единице объема, скорости которых попадают в интервал скоростей Dv x Dv y Dv z . Для нахождения интервала скоростей построим воображаемое пространство скоростей (v x v y v z ) и отложим там значения компонентов скоростей v x , v y, v z отдельных молекул. Тогда каждой молекуле будет соответст
где B - постоянная величина, Dn - число молекул в единице объема, скорости которых попадают в интервал скоростей Dv x Dv y Dv z . Для нахождения интервала скоростей построим воображаемое пространство скоростей (v x v y v z ) и отложим там значения компонентов скоростей v x , v y, v z отдельных молекул. Тогда каждой молекуле будет соответст  вовать точка в этом пространстве (рис.9.4). Расположение точек относительно начала координат вследствие равноправности всех направлений движения будет сферически симметричным. Выберем элемент объема скоростей лежащим между двумя сферическими поверхностями с радиусами v и (v + Dv), получим его равным 4pv 2 Dv. Тогда, подставляя 4pv 2 Dv вместо DvxDvyDvz, запишем (9.17) в виде
вовать точка в этом пространстве (рис.9.4). Расположение точек относительно начала координат вследствие равноправности всех направлений движения будет сферически симметричным. Выберем элемент объема скоростей лежащим между двумя сферическими поверхностями с радиусами v и (v + Dv), получим его равным 4pv 2 Dv. Тогда, подставляя 4pv 2 Dv вместо DvxDvyDvz, запишем (9.17) в виде (9.19)
(9.19) где С - постоянная величина. Введем величину
где С - постоянная величина. Введем величину Приравняв производную от выражения (9.21) по u нулю, получим экстремальные значения u, равные u = 0, u = 1, u =
Приравняв производную от выражения (9.21) по u нулю, получим экстремальные значения u, равные u = 0, u = 1, u =  . Зависимость f(v) от v для различных температур T1 и T2 показана на рис. 9.5. Кривая имеет максимум, соответствующий величине u = 1. Скорость, соответствующая максимуму кривой, называется наиболее вероятной и обозначается символом v нв. По определению f(v) показывает, какая часть молекул имеет скорости в единичном интервале скоростей (Dv = 1). Если взять скорость молекулы в какой-либо момент времени, то наиболее вероятным значением скорости будет v нв, так как функция f (v) для этого значения скорости имеет максимальное значение. Приравняв выражение (9.20) единице, получим mv нв 2/(2kT) = 1 или
. Зависимость f(v) от v для различных температур T1 и T2 показана на рис. 9.5. Кривая имеет максимум, соответствующий величине u = 1. Скорость, соответствующая максимуму кривой, называется наиболее вероятной и обозначается символом v нв. По определению f(v) показывает, какая часть молекул имеет скорости в единичном интервале скоростей (Dv = 1). Если взять скорость молекулы в какой-либо момент времени, то наиболее вероятным значением скорости будет v нв, так как функция f (v) для этого значения скорости имеет максимальное значение. Приравняв выражение (9.20) единице, получим mv нв 2/(2kT) = 1 или . (9.22)
. (9.22) v нв).
v нв). . Подставляя сюда (9.21), получим v ср =
. Подставляя сюда (9.21), получим v ср =  v нв или с учетом (9.22)
v нв или с учетом (9.22) . (9.23)
. (9.23)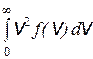 = 3kT/m.
= 3kT/m.


