
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопроводность. Закон Фурье. Коэффициент теплопроводности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Необходимым условием распространения теплоты являетсянеравномерность распределения температуры в рассматриваемой среде. Таким образом, для передачи теплоты теплопроводностью необходимо неравенство нулю температурного градиента в различных точках тела. Закон Фурье:
Согласно закону Фурье количество теплоты проходящий через элемент изотермической поверхности
где Количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности Коэффициент теплопроводности Под коэффициентом теплопроводности понимают тепловой поток, передаваемый через единичную поверхность при единичном значении температурного градиента
Дифференциальное уравнение теплопроводности. Условия однозначности. Распределение температуры в теле, описывается дифференциальным уравнением теплопроводности, которое при принятых допущениях, а именно: тело однородно и изотропно; физические параметры тела постоянны во времени и пространстве; температурные деформации рассматриваемого элементарного объема малы по сравнению с самим объемом; внутренние источники теплоты распределены в рассматриваемом объеме равномерно; макрочастицы тела неподвижны относительно друг друга; имеет следующий вид:
где
Чтобы получить конкретное решение дифференциального уравнения для рассматриваемого случая, необходимо ввести полное математическое описание данного конкретного процесса теплопроводности. Эти частные особенности называются условиями однозначности или краевыми условиями, включающими: · геометрические условия (форма, размеры тела); · Физические условия (физические свойства тела и его физические параметры); · Начальные условия (распределение температуры в теле в начальный момент времени); · Граничные условия, определяющие взаимодействие тела с окружающей средой. 1. Граничные условия первого рода. Задается распределение температуры на поверхности тела, как функция координат и времени
В частном случае, если температура поверхности тела постоянна выражение имеет вид 2. Граничные условия второго рода. Задается распределение плотности теплового потока на поверхности тела, как функция координат и времени
В частном случае, когда плотность теплового потока на поверхности тела остается постоянной, имеем 3. Граничные условия третьего рода. Задается температура окружающей среды
Это уравнение выражает закон Ньютона-Рихмана. Теплота, воспринятая поверхностью тела, распространяется в нем по закону Фурье. Следовательно, где
Индекс “ с” означает, что температурный градиент относится к поверхности тела.
Уравнение является аналитическим выражением граничных условий третьего рода. 4. Граничные условия четвертого рода. Отражают условия теплообмена системы тел имеющих различные значения коэффициентов теплопроводности. Между телами предполагается идеальный контакт. Тогда
где
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.8.126 (0.006 с.) |


 за промежуток времени
за промежуток времени  , пропорционально температурному градиенту
, пропорционально температурному градиенту ,
, – коэффициент пропорциональности есть физический параметр вещества и называется коэффициентом теплопроводности, Вт/(м·°C);
– коэффициент пропорциональности есть физический параметр вещества и называется коэффициентом теплопроводности, Вт/(м·°C);  , называется плотностью теплового потока.
, называется плотностью теплового потока.

 ,
, – время, сек;
– время, сек;  – коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела,
– коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, 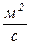 ;
; – теплоемкость тела,
– теплоемкость тела,  ;
;  – плотность тела, кг/м3;
– плотность тела, кг/м3;  – объемная плотность тепловыделения, Bm/м3;
– объемная плотность тепловыделения, Bm/м3;  – оператор Лапласа.
– оператор Лапласа. где
где 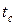 -температура поверхности тела.
-температура поверхности тела.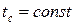 .
. .
. .
. и закон теплообмена между поверхностью тела и окружающей средой
и закон теплообмена между поверхностью тела и окружающей средой если
если  .
. – коэффициент теплообмена, представляющий собой плотность теплового потока подведенного (отведенного) к единице поверхности тела при разности температур между поверхностью тела и окружающей среды 1К, Вm/(м2К)
– коэффициент теплообмена, представляющий собой плотность теплового потока подведенного (отведенного) к единице поверхности тела при разности температур между поверхностью тела и окружающей среды 1К, Вm/(м2К) .
. .
. ,
, – коэффициент теплопроводности первого тела;
– коэффициент теплопроводности первого тела;  – коэффициент теплопроводности второго тела.
– коэффициент теплопроводности второго тела.


