
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплоотдача. Закон Ньютона-Рихмана. Коэффициент теплоотдачи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Под конвективным теплообменом понимают форму передачи теплоты при движении жидкости или газа под влиянием двух процессов – конвекции и теплопроводности. Конвекцией называется перенос макрочастиц жидкости в пространстве. Если эти частицы жидкости перемешаются из области с одной температурой в область с другой температурой, их перемещение сопровождается переносом теплоты. Перенос теплоты конвекцией сопровождается теплопроводностью при непосредственном соприкосновении различно нагретых частиц жидкости. Количество теплоты, отдаваемое жидкостью твердой стенке или воспринимаемое жидкостью от стенки в единицу времени, определяется уравнением Ньютона –Рихмана:
а плотность теплового потока следующим образом:
где α – коэффициент, характеризующий условия теплообмена между жидкостью и поверхностью твердого тела, называемый коэффициентом теплоотдачи, Вт/(м2·°C); В соответствии с формулой плотности теплового потока по своему физическому смыслу коэффициент теплоотдачи есть плотность теплового потока (q) на поверхности тела, отнесенная к разности температур поверхности тела и окружающей среды. Коэффициент теплоотдачи численно равен плотности теплового потока при температурном напоре, равном единице. Коэффициент теплоотдачи зависит от многих факторов. В наиболее общем случае является функцией формы и размера тела, режима движения жидкости, физических свойств жидкости, положения в пространстве и состояния поверхности теплообмена и других величин. Процесс теплоотдачи в зависимости от природы движения жидкости протекает различно. Дифференциальные уравнения конвективного теплообмена. Основные понятия. Дифференциальное уравнение теплообмена получается при рассмотрении передачи теплоты теплопроводностью через, практический, неподвижный слой жидкости (пограничный слой), который имеет место вблизи твердого тела, омываемого жидкостью (
Дифференциальное уравнение энергии при условии однородности и несжимаемости жидкости, отсутствия внутренних источников теплоты и работы расширения, а также постоянства физических параметров жидкости в пределах элементарного объема формулируется следующим образом:
Дифференциальное уравнение неразрывности получается на основе закона сохранения массы и, для сжимаемой жидкости имеет следующий вид:
Уравнение движения (уравнение Навье-Стокса) получается на базе первого и второго законов Ньютона и в векторной форме записи можно представить в виде
Понятия о теории подобия. Для подобия физических процессов необходимо говорить о подобии физических величин и явлений. Два или несколько явлений будут подобны, если подобны все физические величины, характеризующие эти явления, т.е. подобные между собою явления имеют одинаковые безразмерные комплексы - критерии подобия. Этот вывод свидетельствует о том, что в опытах нужно измерять те величины, которые входят в критерии подобия, характеризующие данный процесс. Важной теоремой теории подобия является утверждение о том, что решение дифференциального уравнения, описывающего данный процесс, может быть представлено в виде функциональной зависимости между критериями подобия, характеризующими этот процесс и полученными из исходного уравнения. Это утверждение говорит о том, опытные данные надо обработать в виде зависимости между критериями подобия. Наряду с приведенными выше двумя теоремами подобия, важным является и утверждение о том, что подобны между собой те явления, которые принадлежат к одному классу, к одному роду и имеют равные определяющие критерии подобия. Этот вывод позволяет полученные в опыте расчетные зависимости распространить на группу явлений, подобных исследованному. Таким образом, теория подобия, при наличии дифференциальных уравнений, описывающих рассматриваемый процесс, позволяет, не решая сами уравнения, получить выражения чисел (критериев) подобия и на их основе получить расчетные зависимости – уравнения подобия.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 - основное уравнение теплоотдачи.
- основное уравнение теплоотдачи.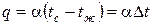
 – температурный напор, K.
– температурный напор, K.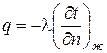 ) и передачи теплоты к пограничному слою за счет конвективного теплообмена (
) и передачи теплоты к пограничному слою за счет конвективного теплообмена ( ):
):







