Ранговые коэффициенты связи.
Содержание книги
- Макроэкономика. Микроэкономика. Мировая экономика.
- Экономический выбор и альтернативная стоимость(возможность).
- Общая и предельная полезность блага.
- Отдача от масштаба производства.
- Бухгалтерская и экономическая прибыль.
- Особенности рынка несовершенной конкуренции
- Земля как фактор производства.
- Неоклассическая кривая совокупного предложения в долгосрочном периоде.
- Денежная масса, ее структура и измерение
- Сущность и виды безработицы.
- Антиинфляционная политика: классический и кейнсианский подход
- Концепции стадий экономического роста
- Средние характеристики ряда динамики
- Оценка существенности связи.
- Ранговые коэффициенты связи.
- Изучение состава населения по демографическим, этническим, социально-экономическим признакам.
- Распределение доходов и социально-экономическая дифференциация населения.
- Определение основных видов прибыли: валовая прибыль, прибыль от продаж, прибыль до налогообложения, прибыль от обычных видов деятельности, чистая (нераспределенная) прибыль.
- Рыночная концентрация: монопольная власть и доминирующее положение фирмы
- Максимизация прибыли монополии, последствия монопольной власти.
- Механизм государственного регулирования естественных монополий
- Регулирование деятельности естественных монополий
- Причины, сдерживающие развитие российского страхового бизнеса.
- Основные средства, их характеристика, классификация, оценка и переоценка, нормативное регулирование их учета
- Особенности учета деловой репутации
- Формирование фактической себестоимости материалов, поступающих на склад
- Раскрытие информации о запасах материальных ценностей в бухгалтерской отчетности
- Учет выплаты заработной платы и депонированных сумм
- Аналитический и синтетический учет кассовых операций
- Разновидности метода: способ цепных подстановок, способ абсолютных и относительных (процентных) отклонений, индексный, интегральный. Алгоритмы расчетов, достоинства и недостатки.
- Анализ факторов, влияющих на прибыль от реализации продукции: себестоимости, цен, объема, структуры ассортимента.
- Источники информации и методы анализа(платежеспособность и ликвидность)
- Финансовая политика государства, факторы ее определяющие
- Роль и место бюджета в системе государственных финансов; принципы организации и структура бюджетной системы РФ.
- Неналоговые доходы бюджетов бюджетной системы РФ (ст. 41, 42, 46, 51, 57, 62 бк РФ).
- Безвозмездные поступления (ст. 41 П. 4 бк РФ).
- Объект и субъект налогообложения.
- Участники бюджетного процесса и их характеристика.
- Роль центрального банка в регулировании денежного оборота и денежной массы
- Специализированные небанковские финансово-кредитные институты – цели создания, функции, выполняемые операции.
Похожие статьи вашей тематики
В анализе массовых процессов и явлений часто приходится прибегать к различным условным оценкам, которые называются рангами, а взаимосвязь между отдельными признаками измерять с помощью непараметрических коэффициентов связи. Эти коэффициенты исчисляются при условии, что исследуемые признаки подчиняются различным законам распределения.
Ранжирование - процедура упорядочивания объектов изучения, которая выполняется на основе предпочтения.
Ранг - порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количественную оценку, то ранг всех этих значений принимается равным средней арифметической от соответствующих номеров мест, которые они определяют. Данные ранги называются связными.
Среди непараметрических методов оценки тесноты связи наибольшее значение имеют ранговые коэффициенты Спирмена (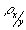 ) и Кендала ( ) и Кендала ( ). Эти коэффициенты могут быть использованы для определения тесноты связей как между количественными, так и между качественными признаками при условии, если их значения упорядочить или проранжировать по степени убывания или возрастания признака. ). Эти коэффициенты могут быть использованы для определения тесноты связей как между количественными, так и между качественными признаками при условии, если их значения упорядочить или проранжировать по степени убывания или возрастания признака.
Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается для случаев, когда нет связных рангов. Его формула:

где  - квадрат разности рангов; - квадрат разности рангов;
n - число наблюдений (число пар рангов).
Коэффициент Спирмена принимает любые значения в интервале (-1;1). Значимость коэффициента корреляции рангов Спирмена проверяется на основе критерия Стьюдента.
Расчет коэффициента Спирмена осуществляется по следующему алгоритму. Сначала ранжируются значения результирующего признака. Затем ранжируются значения факторного признака. Значения рангов парных признаков: результирующего и факторного сравниваются, вычисляется разница рангов, которая возводится в квадрат и далее подставляется в формулу.
Ранговый коэффициент корреляции Кендалла может использоваться для измерения взаимосвязи между качественными и количественными признаками, характеризующими однородные объекты. Ранжированные по одному принципу. Расчет рангового коэффициента Кендалла осуществляется по формуле

где n- число наблюдений;
S - сумма разностей между числом последовательностей и числом инверсий по второму признаку. S = P + Q
Расчет данного коэффициента выполняется в следующей последовательности:
1) значения Х ранжируются в порядке возрастания или убывания;
2) значения У располагаются в порядке, соответствующем значениям Х;
3) для каждого ранга У определяется число следующих за ним рангов, превышающих его величину. Суммируя таким образом числа, определяется величина Р как мера соответствия последовательностей рангов Х и У и учитывается со знаком (+);
4) для каждого ранга У определяется число следующих за ним рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком (-);
5) определяется сумма баллов по всем членам ряда.
Формула Кендалла используется и для связных рангов.
Как правило коэффициент Кендалла меньше коэффициента Спирмена.
Связь между признаками можно признать статистически значимой, если значения коэффициентов ранговой корреляции Спирмена и Кендалла больше 0.5.
Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции (коэффициент конкордации) (W), который вычисляется по формуле:

где m - количество факторов;
n - число наблюдений;
S - отклонение суммы квадратов рангов от средней квадратов рангов.
Коэффициент конкордации принимает любые значения в интервале (-1;1).
Ранговые коэффициенты корреляции Спирмена, Кендалла и конкордации обладают тем преимуществом, что с их помощью можно измерять и оценивать связи как между количественными, так и между атрибутивными признаками, которые поддаются ранжированию.
Статистика цен.
|