
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Коэффициент корреляции рангов Спирмена, его применениеСодержание книги
Поиск на нашем сайте Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента. Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы: 1) Сопоставать каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию). 2) Определить разности рангов каждой пары сопоставляемых значений. 3) Возвести в квадрат каждую разность и суммировать полученные результаты. 4) Вычислить коэффициент корреляции рангов по формуле:.
где При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента равные 0,3 и менее, показателями слабой тесноты связи; значения более 0,4, но менее 0,7 - показателями умеренной тесноты связи, а значения 0,7 и более - показателями высокой тесноты связи. Мощность коэффициента ранговой корреляции Спирмена несколько уступает мощности параметрического коэффициента корреляции. Коэффицент ранговой корреляции целесообразно применять при наличии небольшого количества наблюдений. Данный метод может быть использован не только для количественно выраженных данных, но также и в случаях, когда регистрируемые значения определяются описательными признаками различной интенсивности.
Дисперсия и среднее квадратическое (стандартное) отклонение Среднеквадратическое отклонение показывает абсолютное отклонение измеренных значений от среднеарифметического. В соответствии с формулой для меры точности линейной комбинации средняя квадратическая ошибка среднего арифметического определяется по формуле:
Наиболее простым и достаточно точно отображающим действительность (в подавляющем большинстве случаев) является так называемый нормальный закон распределения ошибок:
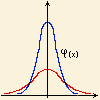
Этот закон распределения может быть получен из различных теоретических предпосылок, в частности, из требования, чтобы наиболее вероятным значением неизвестной величины, для которой непосредственным измерением получен ряд значений с одинаковой степенью точности, являлось среднее арифметическое этих значений. Величина T-распределение Стьюдента Распределение Стьюдента по сути представляет собой сумму нескольких нормально распределенных случайных величин. Чем больше величин, тем больше верятность, что их сумма будет иметь нормальное распределение. Таким образом, количество суммруемых величин определяет важнейший параметр формы данного распредения - число степеней свободы (DL). График слева показывает, как меняется форма распределения при увеличение количества степеней свободы (DL).
Распределе́ние Стью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений.
Пусть
называется распределением Стьюдента с
где Свойства распределения Стьюдента
Связь с другими распределениями
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.005 с.) |

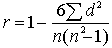
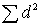 - сумма квадратов разностей рангов, а
- сумма квадратов разностей рангов, а  - число парных наблюдений.
- число парных наблюдений.

 2 называется дисперсией данного нормального закона.
2 называется дисперсией данного нормального закона. — независимые стандартные нормальные случайные величины, такие что
— независимые стандартные нормальные случайные величины, такие что  . Тогда распределение случайной величины
. Тогда распределение случайной величины 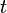 , где
, где
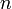 степенями свободы. Пишут
степенями свободы. Пишут  . Её распределение абсолютно непрерывно и имеет плотность
. Её распределение абсолютно непрерывно и имеет плотность ,
,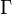 — гамма-функция Эйлера.
— гамма-функция Эйлера.
 .
.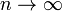 . Пусть дана последовательность случайных величин
. Пусть дана последовательность случайных величин  , где
, где 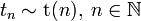 . Тогда:
. Тогда:  по распределению при
по распределению при 


