
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полигон распределения и гистограммаСодержание книги
Поиск на нашем сайте
Ряд распределения — представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку. Частоты — это абсолютные числа, показывающие столько раз в совокупности встречается данное значение признака, которые обозначают Ряды распределения изображаются в виде:
При построении полигона на горизонтальной оси (ось абсцисс) откладывают значения варьирующего признака, а на вертикальной оси (ось ординат) — частоты или частости. Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков в случае равных интервалов должна быть пропорциональна частотам. В результате мы получим гистограмму - график, на котором ряд распределения изображен в виде смежных друг с другом столбиков. Индексы постоянного и переменного состава и индекс структурных сдвигов Индекс переменного состава – это относительная величина, характеризующая динамику двух средних показателей для однородных совокупностей. Этот индекс отражает влияние двух факторов: – изменение индексируемого показателя у отдельных объектов (частей целого); – изменение удельного веса этих частей в общей структуре совокупностей. Индекс фиксированного состава – характеризует динамику двух средних величин при одинаковой фиксированной структуре совокупности в отчетном периоде. Индекс структурных сдвигов – это отношение двух средних величин, рассчитанных для разной структуры совокупности, но при постоянной величине индексируемого показателя в базисном периоде. В экономических финансовых исследованиях получили широкое распространение средние показатели: средняя цена, средняя заработная плата, средняя себестоимость и т.д.
При динамическом анализе средних показателей используют систему индексов, состоящих из индекса переменного состава, индекса фиксированного (постоянного состава) и индекса структурных сдвигов. Данная система индексов позволяет решить задачу изменения структуры от изменения качественных показателей, а также позволяет выявить влияние факторов на индексируемую величину. Система индексов используется, когда соизмеримая продукция производится на разных участках. Кумулятивная функция
Функция Теорема 1. Функция распределения FX (x) любой случайной величины удовлетворяет следующим трем свойствам:
Из того факта, что борелевская сигма-алгебра на вещественной прямой порождается семейством интервалов вида Теорема 2. Любая функция F (x), удовлетворяющая трём свойствам, перечисленным выше, является функцией распределения для какого-то распределения Для вероятностных распределений, обладающих определенными свойствами, существуют более удобные способы его задания. В теория вероятности и статистик, кумулятивная функция распределения (Также вызванное CDF), функция распределения вероятности или как раз функция распределения,[1] вполне описывает распределение вероятности вещественнозначного произвольнаяой переменнаи X. Методы сглаживания частот Сглаживание. Сглаживание всегда включает некоторый способ локального усреднения данных, при котором несистематические компоненты взаимно погашают друг друга. Самый общий метод сглаживания - скользящее среднее, в котором каждый член ряда заменяется простым или взвешенным средним n соседних членов, где n - ширина "окна" (см. Бокс и Дженкинс, 1976; Velleman and Hoaglin, 1981). Вместо среднего можно использовать медиану значений, попавших в окно. Основное преимущество медианного сглаживания, в сравнении со сглаживанием скользящим средним, состоит в том, что результаты становятся более устойчивыми к выбросам (имеющимся внутри окна). Таким образом, если в данных имеются выбросы (связанные, например, с ошибками измерений), то сглаживание медианой обычно приводит к более гладким или, по крайней мере, более "надежным" кривым, по сравнению со скользящим средним с тем же самым окном. Основной недостаток медианного сглаживания в том, что при отсутствии явных выбросов, он приводит к более "зубчатым" кривым (чем сглаживание скользящим средним) и не позволяет использовать веса.
Относительно реже, когда ошибка измерения очень большая, используется метод сглаживания методом наименьших квадратов, взвешенных относительно расстояния или метод отрицательного экспоненциально взвешенного сглаживания. Все эти методы отфильтровывают шум и преобразуют данные в относительно гладкую кривую (см. соответствующие разделы, где каждый из этих методов описан более подробно). Ряды с относительно небольшим количеством наблюдений и систематическим расположением точек могут быть сглажены с помощью бикубических сплайнов.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.83.45 (0.008 с.) |

 . Сумма всех частот равна должна быть равна численности единиц всей совокупности.
. Сумма всех частот равна должна быть равна численности единиц всей совокупности.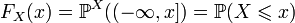 называется (кумулятивной) функцией распределения случайной величины X. Из свойств вероятности вытекает
называется (кумулятивной) функцией распределения случайной величины X. Из свойств вероятности вытекает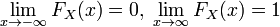 ;
; , вытекает
, вытекает .
.


