
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Почему нельзя сравнивать коэффициенты регрессии в натуральном масштабеСодержание книги
Поиск на нашем сайте
Почему нельзя сравнивать коэффициенты регрессии в натуральном масштабе Регрессио́нный (линейный) анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X 1, X 2,..., Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными.
Цели и задачи статистики Предметом статистической науки являются: 1) массовые социально–экономические явления жизни; 2) количественная сторона этих явлений в конкретных условиях места и времени. Посредством статистических показателей статистика изучает все явления и процессы, протекающие в жизни общества. Основные задачи статистической науки: 1) исследовать происходящие в обществе преобразования социально–экономических процессов; 2) выявить резервы эффективности общественного производства; 3) своевременно обеспечить органы законодательной власти надежной информацией. Ставит своей целью установить и измерить закономерности явления в целом и рассматривает единичные факты лишь как необходимые элементы исследуемой совокупности. Так, для получения обобщенной количественной характеристики по тому или иному экономическому вопросу (например, чтобы установить влияние экономической реформы на снижение себестоимости, повышение производительности труда и Др.) в масштабе предприятия, объединения, министерства и, наконец, всего народного хозяйства необходима статистическая обработка данных оперативного и бухгалтерского учета. ?3. В каких случаях параметр а можно содержательно интерпретировать? Параметры bi являются частными коэффициентами корреляции; (bi)2 интерпретируется как доля дисперсии Y, объяснённая Xi, при закреплении влияния остальных предикторов, то есть измеряет индивидуальный вклад Xi в объяснение Y. В случае коррелирующих предикторов возникает проблема неопределённости в оценках, которые становятся зависимыми от порядка включения предикторов в модель. В таких случаях необходимо применение методов анализа корреляционного и пошагового регрессионного анализа. Говоря о нелинейных моделях регрессионного анализа, важно обращать внимание на то, идет ли речь о нелинейности по независимым переменным (с формальной точки зрения легко сводящейся к линейной регрессии), или о нелинейности по оцениваемым параметрам (вызывающей серьёзные вычислительные трудности). При нелинейности первого вида с содержательной точки зрения важно выделять появление в модели членов вида X 1 X 2, X 1 X 2 X 3, свидетельствующее о наличии взаимодействий между признаками X 1, X 2 и т. д. Какие виды выборочного наблюдения вам известны? В статистике различают следующие виды выборок: 1. Собственно случайная выборка, суть которой состоит в том, что отбирают единицы по жребию. Отбор осуществляется повторный и бесповторный. Повторный отбор, при котором единицы совокупности участвуют столько раз, сколько происходит наблюдение. Бесповторный отбор – единица, выбранная раз, больше не участвует. 2. Механическая выборка. Генеральную совокупность механически разбивают на столько частей, сколько надо отобрать в выборку, а затем из каждой части механически отбирают единицы. Механическая выборка производится только бесповторным способом. 3. Типическая выборка. Генеральная совокупность также разбивается на группы, но обязательно по какому-то признаку, а затем из каждой группы случайным или механическим способом отбирают нужное число единиц. 4. Серийная. Отбирают не отдельные единицы, а целые группы или серии. Затем обследуют все единицы отобранных групп. Способ отбора случайный, либо механический, но бесповторным способом. 5. Многоступенчатая выборка. Типически отобранная часть сочетается с несколькими стадиями или ступенями отбора, причем на каждой ступени выбирается своя единица. 6. Многоразовая. Сохраняется одна и та же единица совокупности. 7. Комбинированная. Выборочное наблюдение сочетается со сплошным. 8. Моментное наблюдение. Фиксируются не единицы совокупности, а состояние явления. 9. Малая выборка. Число единиц до 20. Выборочное наблюдение относится к разновидности несплошного наблюдения. Оно охватывает отобранную часть единиц генеральной совокупности. Цель выборочного наблюдения - по отобранной части единиц дать характеристику всей совокупности единиц. Чтобы отобранная часть была репрезентативна (т.е. представляла всю совокупность единиц), выборочное наблюдение должно быть специально организовано. Следовательно, в отличие от генеральной совокупности, представляющей всю совокупность исследуемых единиц, выборочная совокупность представляет ту часть единиц генеральной совокупности, которая является объектом непосредственного наблюдения. Кластерный анализ как статистический метод Кластерный анализ (англ. Data clustering) — задача разбиения заданной выборки объектов (ситуаций) на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. Задача кластеризации относится к статистической обработке, а также к широкому классу задач обучения без учителя. Кластерный анализ — это многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы (кластеры)(Q-кластеризация, или Q-техника, собственно кластерный анализ). Кластер — группа элементов, характеризуемых общим свойством, главная цель кластерного анализа — нахождение групп схожих объектов в выборке Медиана, мода, квартили, особенности применения Медиа́на (50-й процентиль, квантиль 0,5) — возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана. Медиана является важной характеристикой распределения случайной величины и так же, как математическое ожидание, может быть использовано для центрирования распределения. Однако, медиана более робастна и поэтому может быть более предпочтительной для распределений с т.н. тяжёлыми хвостами. Медиана определяется для широкого класса распределений (например, для всех непрерывных), а в случае неопределённости, естественным образом доопределяется (см. ниже), в то время как математическое ожидание может быть не определено (например, у распределения Коши). Для дискретного рядораспределения с нечётным количеством членов n номер медианного варианта определяется как (n-1)/2. Если n четная, то медианой будет являются среднее значение 2 вариантов n/2 и n/2-1. Медиана равна 680 000 руб. Расчёт медианы в интервальном ряду распределения осуществляется в 2 этапа. Выделяется медианный интервал и рассчитывается значение медианы по формуле. Ме=Xme+hme ((∑f)/2-Sme-1)/Fme
Под модой в статистике понимается значение признака или вариант, который чаще всего встречается в данной совокупности. В дискретном ряду распределения модой является вариант, обладающий наибольшей частотой. Выбирается модальный интервал. Рассчитывается значение моды по формуле M_O=x_n+[h_(M_O)]*(Fmo-Fmo-1)/((Fmo-fmo-1)+(Fmo-Fmo+1)) Кванти́ль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированной вероятностью. квартиль - это линии, отсекающие по 25% какого-то множества значений Индексы и их классификация Слово «индекс» в переводе с латинского (index) означает «указатель», «показатель». Как видели выше, этот статистический показатель используется для целей сопоставительного анализа развития явления во времени, т.е. является относительной величиной. 1) В зависимости от характера объектов исследования различают индексы объемных и индексы качественных показателей. 2) По степени охвата элементов (единиц) совокупности индексы делятся на индивидуальные, групповые и общие. Кумулятивная функция
Функция Теорема 1. Функция распределения FX (x) любой случайной величины удовлетворяет следующим трем свойствам:
Из того факта, что борелевская сигма-алгебра на вещественной прямой порождается семейством интервалов вида Теорема 2. Любая функция F (x), удовлетворяющая трём свойствам, перечисленным выше, является функцией распределения для какого-то распределения Для вероятностных распределений, обладающих определенными свойствами, существуют более удобные способы его задания. В теория вероятности и статистик, кумулятивная функция распределения (Также вызванное CDF), функция распределения вероятности или как раз функция распределения,[1] вполне описывает распределение вероятности вещественнозначного произвольнаяой переменнаи X. Методы сглаживания частот Сглаживание. Сглаживание всегда включает некоторый способ локального усреднения данных, при котором несистематические компоненты взаимно погашают друг друга. Самый общий метод сглаживания - скользящее среднее, в котором каждый член ряда заменяется простым или взвешенным средним n соседних членов, где n - ширина "окна" (см. Бокс и Дженкинс, 1976; Velleman and Hoaglin, 1981). Вместо среднего можно использовать медиану значений, попавших в окно. Основное преимущество медианного сглаживания, в сравнении со сглаживанием скользящим средним, состоит в том, что результаты становятся более устойчивыми к выбросам (имеющимся внутри окна). Таким образом, если в данных имеются выбросы (связанные, например, с ошибками измерений), то сглаживание медианой обычно приводит к более гладким или, по крайней мере, более "надежным" кривым, по сравнению со скользящим средним с тем же самым окном. Основной недостаток медианного сглаживания в том, что при отсутствии явных выбросов, он приводит к более "зубчатым" кривым (чем сглаживание скользящим средним) и не позволяет использовать веса. Относительно реже, когда ошибка измерения очень большая, используется метод сглаживания методом наименьших квадратов, взвешенных относительно расстояния или метод отрицательного экспоненциально взвешенного сглаживания. Все эти методы отфильтровывают шум и преобразуют данные в относительно гладкую кривую (см. соответствующие разделы, где каждый из этих методов описан более подробно). Ряды с относительно небольшим количеством наблюдений и систематическим расположением точек могут быть сглажены с помощью бикубических сплайнов. Хронологическая Применяется для определения среднего уровня в моментных рядах динамики. Существует два вида рядов динамики: 1. моментные; 2. интервальные. Интервальные — это такие ряды в которых данные приводятся за определенный период времени (месяц, год). Средний уровень ряда в интервальном ряду определяется по средней арифметической простой. Моментные — это такие ряды, где данные представлены на определенный момент времени (на определенную дату). Если интервалы времени между датами равны, то расчет средней ведут по формуле средней хронологической простой. Пример. Моментный ряд:
чел. Если интервалы между датами в моментных рядах не одинаковые, то расчет ведется в два этапа: по средней хронологической взвешенной 1. определяется средняя внутри каждого интервала времени по среднеарифметической простой; 2. определяется общая средняя по среднеарифметической взвешенной, где частотами являются интервалы между датами. Тот же, что и вопрос 5 T-распределение Стьюдента Распределение Стьюдента по сути представляет собой сумму нескольких нормально распределенных случайных величин. Чем больше величин, тем больше верятность, что их сумма будет иметь нормальное распределение. Таким образом, количество суммруемых величин определяет важнейший параметр формы данного распредения - число степеней свободы (DL). График слева показывает, как меняется форма распределения при увеличение количества степеней свободы (DL).
Распределе́ние Стью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений.
Пусть
называется распределением Стьюдента с
где Почему нельзя сравнивать коэффициенты регрессии в натуральном масштабе Регрессио́нный (линейный) анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X 1, X 2,..., Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными.
Цели и задачи статистики Предметом статистической науки являются: 1) массовые социально–экономические явления жизни; 2) количественная сторона этих явлений в конкретных условиях места и времени. Посредством статистических показателей статистика изучает все явления и процессы, протекающие в жизни общества. Основные задачи статистической науки: 1) исследовать происходящие в обществе преобразования социально–экономических процессов; 2) выявить резервы эффективности общественного производства; 3) своевременно обеспечить органы законодательной власти надежной информацией. Ставит своей целью установить и измерить закономерности явления в целом и рассматривает единичные факты лишь как необходимые элементы исследуемой совокупности. Так, для получения обобщенной количественной характеристики по тому или иному экономическому вопросу (например, чтобы установить влияние экономической реформы на снижение себестоимости, повышение производительности труда и Др.) в масштабе предприятия, объединения, министерства и, наконец, всего народного хозяйства необходима статистическая обработка данных оперативного и бухгалтерского учета. ?3. В каких случаях параметр а можно содержательно интерпретировать? Параметры bi являются частными коэффициентами корреляции; (bi)2 интерпретируется как доля дисперсии Y, объяснённая Xi, при закреплении влияния остальных предикторов, то есть измеряет индивидуальный вклад Xi в объяснение Y. В случае коррелирующих предикторов возникает проблема неопределённости в оценках, которые становятся зависимыми от порядка включения предикторов в модель. В таких случаях необходимо применение методов анализа корреляционного и пошагового регрессионного анализа. Говоря о нелинейных моделях регрессионного анализа, важно обращать внимание на то, идет ли речь о нелинейности по независимым переменным (с формальной точки зрения легко сводящейся к линейной регрессии), или о нелинейности по оцениваемым параметрам (вызывающей серьёзные вычислительные трудности). При нелинейности первого вида с содержательной точки зрения важно выделять появление в модели членов вида X 1 X 2, X 1 X 2 X 3, свидетельствующее о наличии взаимодействий между признаками X 1, X 2 и т. д.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 223; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.104.132 (0.008 с.) |

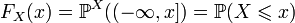 называется (кумулятивной) функцией распределения случайной величины X. Из свойств вероятности вытекает
называется (кумулятивной) функцией распределения случайной величины X. Из свойств вероятности вытекает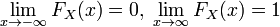 ;
; , вытекает
, вытекает .
. — независимые стандартные нормальные случайные величины, такие что
— независимые стандартные нормальные случайные величины, такие что  . Тогда распределение случайной величины
. Тогда распределение случайной величины 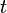 , где
, где
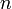 степенями свободы. Пишут
степенями свободы. Пишут  . Её распределение абсолютно непрерывно и имеет плотность
. Её распределение абсолютно непрерывно и имеет плотность ,
,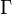 — гамма-функция Эйлера.
— гамма-функция Эйлера.


