
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средние характеристики ряда динамикиСодержание книги
Поиск на нашем сайте
Средний абсолютный прирост рассчитывается как средняя арифметическая из показателей скорости роста за отдельные промежутки времени:
Напомним, число уровней ряда равно Средний коэффициент роста вычисляется по формуле средней геометрической из показателей коэффициентов роста за отдельные периоды:
Средний коэффициент роста показывает, во сколько раз в среднем за отдельные составляющие рассматриваемого периода изменялись уровни динамического ряда. Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах:
Средний темп роста, рассчитанный по данным о конечном и начальном уровнях временного ряда, можно использовать только в случае более или менее равномерного изменения уровней.
Краткое содержание методов (графический метод, скользящей средней, аналитическое выравнивание, модели сезонных колебаний). Способы построения графиков различны для интервальных и дискретных рядов. Графически дискретный вариационный ряд можно изобразить, используя прямоугольную систему координат и строя точки с координатами (х1, f1,),(x2, f2), … (xn, fn). Если затем соединить последовательно полученные точки отрезками прямой, а из первой и последней точек опустить перпендикуляр на ось Х, получим фигуру, которая называется полигоном и графически представляет распределение единиц совокупности по признаку Х.Полученный график (полигон) четко отражает характер рассматриваемого распределения. Сумма частот (частостей), заключенных в полигоне, равна объему совокупности. График интервального ряда, так же как и дискретного ряда, позволяет выявить характер (структуру) распределения изучаемого явления. При построении графика интервального ряда на оси абсцисс откладываются интервалы ряда. Незакрытые интервалы принимаются равными или величине следующего (для открытого первого), или предыдущего (для открытого последнего интервала). Такой прием применяется, если действительные нижняя или верхняя границы этих интервалов неизвестны даже предположительно. Нередко для первого интервала началом принимают “0”. Приняв интервалы за основание, строим на них прямоугольники, равные по высоте частоте данного интервала. Полученное графическое представление интервального вариационного ряда называется гистограммой. Площадь гистограммы, как и полигона, равна объему совокупности.
Метод простой скользящей средней. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда(интервал), затем средний уровень из такого же числа уровней, начиная со второго, далее – начиная с третьего и т.д. Таким образом, при расчете средних уровней они как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень вначале и добавляя один следующий. Интервал может быть нечетным (3, 5, 7 и т.д. точек) или четным (2, 4, 6 и т.д. точек). При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала, при четном этого делать нельзя. Поэтому при обработке ряда четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только 50 %. Недостаток методики сглаживания скользящими средними состоит в условности определения сглаженных уровней для точек в начале и конце ряда. Получают их специальными приемами – расчетом средней арифметической взвешенной. Аналитическое выравнивание. Под этим понимают определение основной проявляющейся во времени тенденции развития изучаемого явления. При таком подходе изменение явления связывают лишь с течением времени, считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющийся во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически. В результате приходят к трендовой модели
В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название«сезонных колебаний» или «сезонных волн», а динамический ряд в этом случае называют тренд-сезонным, или просто сезонным рядом динамики. Сезонные колебания характеризуются специальным показателями, которые называются индексами сезонности (Is). Для выявления сезонных колебаний обычно берут данные за несколько лет, распределенные по месяцам или кварталам. Данные за несколько лет (обычно не менее трех) берутся для того, чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года.Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по фактическим данным без их предварительного выравнивания.Для каждого месяца определяется средняя величина уровня, например, за три года (уi), затем из них рассчитывается среднемесячный уровень для всего ряда (у) и в заключение определяется процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, то есть: Is = (yi/y)*100%
|
||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.42.13 (0.007 с.) |



 , а число аналитических показателей равно
, а число аналитических показателей равно  .
.

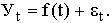 где f(t)– уровень, определяемый тенденцией развития; et – случайное и циклическое отклонение от тенденции. Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t).Чаще всего при выравнивании используются следующие зависимости:
где f(t)– уровень, определяемый тенденцией развития; et – случайное и циклическое отклонение от тенденции. Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости f(t).Чаще всего при выравнивании используются следующие зависимости:



