
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка существенности связи.Содержание книги
Поиск на нашем сайте
Проверка адекватности модели регрессии, построенной на основе того или иного уравнения связи, начинается с проверки значимости каждого коэффициента регрессии. Оценка значимости коэффициентов регрессии осуществляется с помощью t- критерия Стьюдента:
где Параметр модели регрессии признается статистически значимым, если выполняется неравенство:
где
Дисперсия коэффициента регрессии может определяться одним из двух способов:
где
Или:
где
Проверка адекватности всей модели осуществляется с помощью расчета F -критерия и Если средняя ошибка аппроксимации не превышает 12 - 15%, то уравнение построено верно. При проверке адекватности уравнения регрессии исследуемому процессу возможны следующие варианты: 1. Построенная модель на основе ее проверки по критерию Фишера в целом адекватна, и все коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений к осуществлению прогнозов. 2. Модель по критерию Фишера адекватна, но часть коэффициентов регрессии незначима. В этом случае модель пригодна для принятия некоторых решений, но не для прогнозов. 3. Модель по критерию Фишера адекватна, но все коэффициенты регрессии незначимы. Модель в этом случае отвергается. На ее основе никаких решений проводит нельзя. Наиболее сложным этапом, завершающим регрессионный анализ, является интерпретация уравнения регрессии, то есть перевод его с языка статистики и математики на содержательный уровень. С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле:
где
Частный коэффициент детерминации также используется для расширения возможностей содержательного анализа модели регрессии. Он рассчитывается по формуле:
где
Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется вариацией i - го признака, входящего в множественное уравнение регрессии. Рассчитываются также множественный коэффициент детерминации, который представляет собой множественный коэффициент корреляции в квадрате. Он характеризует, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную модель. Рассчитываются также некоторые другие коэффициенты, позволяющие интерпретировать модель регрессии. Отрицательными свойствами уравнений регрессии являются: -хорошо аппроксимируются только те значения результативного признака, которые стоят в середине вариационного ряда индивидуальных значений. Ошибка аппросимации не превышает 1 - 2%; -ошибка аппроксимации на концах исходного ряда может достигать 50%; -уравнения регрессии пригодны только для краткосрочных прогнозов; -на основе уравнения регрессии невозможно получить оптимального значения моделируемого показателя.
|
|||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.101.107 (0.006 с.) |


 - дисперсия коэффициента регрессии.
- дисперсия коэффициента регрессии.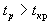 (
( ;
;  =n-k-1)
=n-k-1)
 - дисперсия результативного признака;
- дисперсия результативного признака; - число факторных признаков в уравнении.
- число факторных признаков в уравнении.
 - величина множественного коэффициента корреляции по фактору
- величина множественного коэффициента корреляции по фактору  с остальными факторами;
с остальными факторами;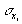 - среднее квадратическое отклонение рассматриваемого фактора;
- среднее квадратическое отклонение рассматриваемого фактора; - среднее квадратическое отклонение результирующего фактора.
- среднее квадратическое отклонение результирующего фактора.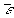 величины средней ошибки аппроксимации.
величины средней ошибки аппроксимации.
 - среднее значение соответствующего факторного признака;
- среднее значение соответствующего факторного признака; - среднее значение результативного признака;
- среднее значение результативного признака;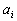 - коэффициент регрессии при соответствующем факторном признаке.
- коэффициент регрессии при соответствующем факторном признаке.
 - парный коэффициент корреляции между результативным и i - факторным признаком;
- парный коэффициент корреляции между результативным и i - факторным признаком; - соответствующий коэффициент уравнения множественной регрессии в стандартизованной форме.
- соответствующий коэффициент уравнения множественной регрессии в стандартизованной форме.


