
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление корреляционной зависимости методом ранговСодержание книги
Поиск на нашем сайте
Коэффициент корреляции методом рангов (Спирмена) вычисляется по формуле:
Для определения достоверности коэффициента корреляции вычисляют: Его ошибку по формуле:
Критерий достоверности (t):
При t равном или больше 3 – коэффициент корреляции достоверен. Пример решения задачи Зависимость между систолическим и диастолическим давлением Дан уровень систолического и диастолического давления (в мм рт. ст.) у 12 здоровых юношей в возрасте 18 лет.
Для вычисления коэффициента ранговой корреляции определяем порядковый номер (ранг), который занимает каждое значение систолического и диастолического давления. При обозначении ранга начинают с меньшего (или большего) значения признака в обоих рядах. Так, например, значение систолического давления 105 мм рт. ст. является наименьшим и мы ставим ранг равный 1. Если значение признака встречается несколько раз ранги проставляются следующим образом: систолическое давление 110 мм рт. ст. встречается 3 раза, занимая по величине 2, 3, 4 места, поэтому порядковый номер в данном случае будет равен (2 + 3 + 4): 3 = 3, т.е. против каждого значения систолического давления, равное 110 мм рт. ст., будет поставлен ранг равный 3, систолическое давление 115 мм рт. ст. встречается 2 раза и против каждого значения будет поставлен ранг (5 + 6): 2 = 5,5 и т.д. Аналогично проставляются ранги и для значений диастолического давления. Затем определяем разность между рангами в каждой строке, обозначив эту разность буквой d, возводим ее в квадрат.
Измерение корреляции между систолическим и диастолическим давлением
Коэффициент ранговой корреляции определяется по формуле:
В нашем примере:
Коэффициент корреляции, равный +0,82, свидетельствует о наличии прямой, сильной связи между систолическим и диастолическим давлением. Для определения достоверности коэффициента корреляции вычисляем: а) его ошибку:
б) критерий достоверности:
Поскольку критерий t больше 3, коэффициент корреляции достоверен. Таким образом, между систолическим и диастолическим давлением существует прямая сильная корреляционная зависимость статистически достотверная
9.3 Контрольные вопросы 1. Что такое корреляционная связь? 2. Чем отличается корреляционная зависимость от функциональной? 3. Какие существуют методы вычисления коэффициента корреляции? 4. Какова оценка силы связи? 5. Как понимать термин «прямая» и «обратная» корреляционная зависимость?
Задача 1 Определите характер и силу связи между загрязненностью воздуха рабочей зоны и частотой возникновения заболеваний органов дыхания, основываясь на данных таблицы. (методом квадратов)
Достоверны ли полученные результаты? Задача 2 Определите, существует ли зависимость между количеством детей в группах дошкольных учреждений и заболеваемостью ОРВИ среди них (см данные таблицы)? (методом рангов)
Задача 3 Определить коэффициент корреляции методом рангов. Длина и масса тела у 7 мальчиков в возрасте 5 лет
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 596; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.109.152 (0.011 с.) |

 , где ρ – коэффициент корреляции, x и y – признаки, между которыми определяется связь, 6 – постоянный коэффициент, n – число наблюдений
, где ρ – коэффициент корреляции, x и y – признаки, между которыми определяется связь, 6 – постоянный коэффициент, n – число наблюдений


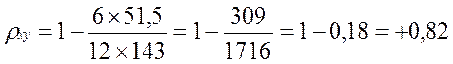










 9.4 Задачи для самостоятельного решения
9.4 Задачи для самостоятельного решения


