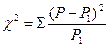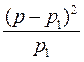Оценка достоверности различия сравниваемых групп по критерию соответствия (хи-квадрат).

При определении характера связи между изучаемыми факторами или явлениями одна из важнейших задач математической статистики заключается в оценке достоверности полученных результатов. Достоверность различий можно оценить по t-критерию, но этот критерий характеризует различия только между двумя совокупностями. При сравнении трех и более совокупностей оценка достоверности при помощи t-критерия затруднительна, так как попарное сравнение не позволяет дать общей оценки различий. Кроме того, сравниваемые группы могут иметь не два результата (да, нет), а несколько. Для решения этой задачи используется критерий «хи-квадрат», разработанный К. Пирсоном. Он же называется коэффициентом согласия и коэффициентом соответствия, «хи-критерием». Он служит для оценки различий в нескольких сравниваемых группах и при нескольких результатах с определенной степенью достоверности (например: оценка различий в распределении детей по частоте заболеваний в районах с разными уровнями загрязнения атмосферного воздуха); определения связи между двумя факторами (результат и зависимый признак). Например, имеется ли связь между жилищными условиями, материальным обеспечением семьи и т. д. и частотой заболеваний, госпитализацией; связь между состоянием физического развития и тяжестью отдельных заболеваний и т. д.; определения идентичности распределения частот двух и более вариационных рядов (коэффициент согласия). Например, одинаково ли распределение частот (детей) по содержанию гемоглобина, количеству эритроцитов, белков крови в двух совокупностях (живущих в зоне загрязнения и «чистой» зоне).

Из приведенных примеров видно, что «хи-квадрат» используется для анализа данных, характеризующих распределение, а не средние величины. Исходный материал для вычислений дается в абсолютных числах по наблюдениям в группах.

Сущность метода «хи-квадрат» заключается в определении достоверности различий между фактическими и теоретическими («ожидаемыми») данными, полученными при условии, что сравниваемые совокупности одинаковы по своему распределению («нулевая гипотеза»). После определения «нулевой гипотезы» на основании этого предположения определяются «ожидаемые» данные, которые сопоставляются с фактическими. Если различий между фактическими и теоретическими числами нет, то нулевая гипотеза подтвердилась и действительно различий в сравниваемых группах нет. Если фактические данные будут отличаться от теоретических, полученных при условии отсутствия различий в распределении, то сравниваемые группы имеют разное распределение и результаты в этих группах статистически достоверно различны.

Таким образом, если Р— фактические данные, P₁ — теоретически исчисленные при нулевой гипотезе, то критерий может быть выражен формулой:

Оценка величины χ² проводится по специальной таблице. Различия считаются достоверными. в том случае, когда величина хи-квадрат соответствует вероятности, меньшей 5% (0,05). Это вероятность подтверждения нулевой гипотезы, т. е. предположения, что различия в сравниваемых группах отсутствуют (связи между факторами нет).

Рассмотрим технику вычисления критерия на примере распределения детей по частоте заболеваний в трех зонах проживания.

Фактические данные (р) представлены в таблице

Распределение детей трех районов по частоте заболеваний

Район проживания	Всего детей	Не болели	Эпизодически болели	Часто болели
Зона химического ком­бината Контрольный район № 1 Контрольный район № 2
Всего...

 

1. Определяем рабочую (нулевую) гипотезу. Предполагается, что в любом месте проживания распределение детей по частоте заболевания будет одинаково. Это распределение вычисляется по итоговой строчке (нулевая гипотеза).

Нулевая гипотеза

Всего детей	Не болели	Эпизодически болели	Часто болели
100%	6,7	46,0	47,3

 

2. В соответствии с нулевой гипотезой вычисляются новые «ожидаемые» данные. Если бы распределение детей по частоте заболевания было бы одинаковым во всех зонах проживания, то число не болевших, эпизодически и часто болевших детей в первой, второй и третьей зонах было бы следующим:

 

 

В зоне химического комбината	В первом контрольном районе
Всего 390 детей	410детей
Не болели 6,7 – 100	6,7 – 100
х – 390	х – 410
Эпизодически болели 46 – 100	46 – 100
х – 390	х – 410
Часто болели 47,3 – 100	47,3 – 100
х – 390	х – 410

 

«Ожидаемые» результаты (теоретические числа)

Район проживания	«Ожидаемые» числа р,	Разница фактических и «ожидаемых» чисел р – р1
не бо­лели	эпизоди­чески болели	часто болели	не бо­лели	эпизоди­чески болели	часто болели
Зона химического комбината Контрольный рай­он № 1 Контрольный рай­он № 2				– 13 +3 + 10	–96 +55 +40	+ 109 –58 –50

 

3. Вычисляется разница фактических и «ожидаемых» чисел, представленная в таблице. Так, при нулевой гипотезе мы ожидали, что в зоне химического комбината число не болевших детей составит 26, эпизодически болевших 179, часто болевших 185. Фактически они составили соответственно: 13, 83, 294.

Различия фактических и «ожидаемых» чисел обусловлены несовпадением нулевой гипотезы и фактического состояния.

4. Различия возводят в квадрат.

5. Вычисляют различия на единицу ожидаемых наблюдений, т. е. квадрат разницы делят на число «ожидаемых» единиц:

Результаты расчетов:

Зоны проживания	(р – р1)^2		(р – р1)^2
	р1
Не болели	Эпизодически болели	Часто болели	Не болели	Эпизодически болели	Часто болели
Зона химического комбината				6,5	51,5	64,2
Контрольный рай­он № 1				0,3	16,1	17,3
Контрольный рай­он № 2				8,7	8,7	13,2

 

Суммируют результаты последнего этапа — расчета: 6,5 + 0,3 + 3,7 + 51,5 + 16,8 и т. д. Сумма составляет—181,5. Это и есть критерий соответствия (χ²).

6. Оценку величины χ² производим по таблице.

Вероятность подтверждения нулевой гипотезы (хи-квадрат)
n'	0,05=5%	0,01=1 %	0,002=0,2%	n'	0,05=5 %	0,01=1%	0,002=0,2 %
I	3,8	6,6	9,5		21,0	26,2	31,0
	6,0	9,2	12,4		22,4	27,7	32,5
	7,8	11,3	14,8		23,7	29,1	34,0
	9,5	13,3	16,9		25,0	30,6	35,5
	11,1	15,1	18,9		26,3	32,0	37,0
	12,6	16,8	20,7		27,6	33,4	38,5
	14,1	18,5	22,6		28,9	34,8	40,0
	15,5	20,1	24,3		30,1	36,2	41,5
	16,9	21,7	26,1		31,4	37,6	43,0
	18,3	23,2	27,7		32,7	38,9	44,5
	19,7	24,7	29,4		33,9	40,3	46,0

 

В первой колонке по вертикали обозначены числа степеней свободы, числа самой таблицы представляют различные величины χ², вверху таблицы даны вероятности подтверждения нулевой гипотезы.

Оценим полученный результат в нашем примере.

Число степеней свободы определяется по формуле:

n'=(S-l) (r-l),

где: S — число сравниваемых групп (строк), r — число групп (граф) результатов.

В нашем исследовании S (число групп детей, проживающих в различных районах загрязнения воздуха) — 3, r (число рассматриваемых параметров их здоровья) — 3 (не болели, эпизодически болели, часто болели),

n'=(3–1) х (3–1)=4.

В четвертой строке таблицы ищем значение χ², соответствующее полученному результату 181,5. Он больше 16,9, значит вероятность нулевой гипотезы в нашем примере менее 0,2%. Правила оценки таковы, что различия считаются достоверными в сравниваемых группах, а также подтверждается наличие связи между результатом и влияющим фактором, если нулевая гипотеза подтверждается с вероятностью меньшей чем 5% (Р<0,05). Если нулевая гипотеза подтверждается с вероятностью большей чем 5% (Р>0,05), то различия считаются недостоверными и связь отсутствующей.

В нашем примере вероятность нулевой гипотезы менее 0,2%, отсюда связь между загрязнением атмосферного воздуха и частотой заболеваний детей имеется и она доказывается с достаточно большой надежностью.