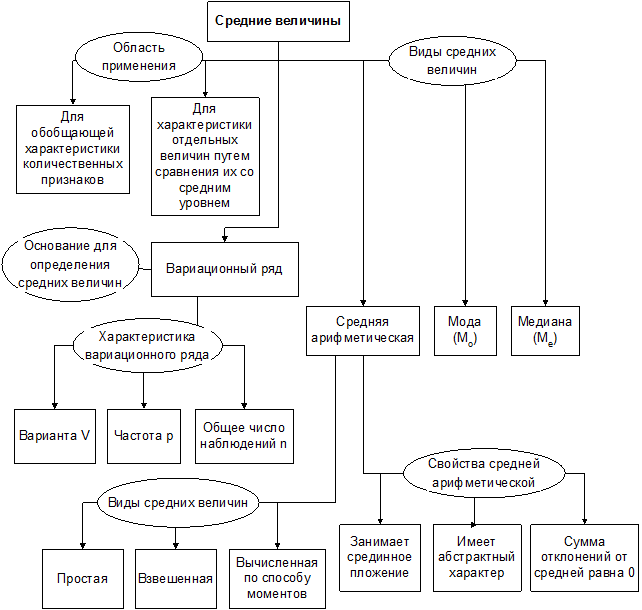
Виды средних величин, методика их вычисления

Различают три вида средних величин: мода (М_о), медиана (M_e), средняя арифметическая (М). Они не могут подменить друг друга и лишь в совокупности достаточно полно и в сжатой форме представляют собой особенности вариационного ряда.

Мода (М_о) — наиболее часто встречающаяся в ряду распределения варианта. Она дает представление о центре распределения вариационного ряда. Используется:

- для определения центра распределения в открытых вариационных рядах

- для определения среднего уровня в рядах с резко асимметричным распределением

Медиана — это серединная варианта, центральный член ранжированного ряда. Название медиана взято из геометрии, где так именуется линия, делящая сторону треугольника на две равные части.

Медиана применяется:

- для определения среднего уровня признака в числовых рядах с неравными интервалами в группах

- для определения среднего уровня признака, когда исход-ные данные представлены в виде качественных признаков и когда единственным способом указать некий центр тяжести совокупности является указание варианты (группы вариант), которая занимает центральное положение

- при вычислении некоторых демографических показателей (средней продолжительности предстоящей жизни)

- при определении наиболее рационального места расположения учреждений здравоохранения, коммунальных учреждений и т. п. (имеется в виду учет оптимальной удаленности учреждений от всех объектов обслуживания)

В настоящее время очень распространены различные опросы ((маркетинговые, социологические и др.), в которых опрашиваемых просят выставить баллы изделиям, политикам и т. п. Затем из полученных оценок рассчитывают средние баллы и рассматривают их как интегральные оценки, выставленные коллективом опрошенных. При этом обычно для определения средних показателей применяют среднее арифметическое. Однако такой способ на самом деле применять нельзя. Обоснованным в этом случае является использование в качестве средних баллов медианы или моды.

Для характеристики среднего уровня признака наиболее часто используется в медицине средняя арифметическая величина (М).

Средняя арифметическая величина — это общая количественная характеристика определенного признака изучаемых явлений, составляющих качественно однородную статистическую совокупность. Различают среднюю арифметическую простую и взвешенную.

Средняя арифметическая простая вычисляется для не сгруппированного вариационного ряда путем суммирования всех вариант и делением этой суммы на общее количество вариант, входящих в вариационный ряд.

Вычисляется средняя арифметическая простая по формуле:

М — средняя арифметическая простая,

ΣV — сумма вариант,

n — число наблюдений

Средняя арифметическая взвешенная вычисляется для сгруппированного вариационного ряда по формуле:

где

М — средняя арифметическая взвешенная,

ΣVp — сумма произведений вариант на их частоты,

n — число наблюдений.

 

Возвращаясь к нашему примеру, определим среднюю частоту пульса (среднее число ударов в минуту) у 54 студентов перед экзаменом.

 

M =	60х1+62х2+64х3+66х3+68х3+70х9+72х6+74х7+76х11+78х5+80х4	=		=72,3 (ударов в минуту)

 

Помимо указанного метода прямого расчета средней арифметической взвешенной, существуют другие методы, в частности, способ моментов при котором несколько упрощены арифметические расчеты.

Расчет средней арифметической способом моментов проводится по формуле:

, где

A – условная средняя (чаще всего в качестве условной средней берется мода М_о)

d – отклонение каждой варианты от условной средней (V–А)

Σdр — сумма произведений отклонений на их частоту.

Порядок вычисления представлен в таблице (за условную среднюю принимаем М_о = 76 ударам в минуту).

Определение средней арифметической способом моментов

 

частота пульса V	Р	d (V–A)	dp
		–16	–16
		–14	–28
		–12	–36
		–10	–30
		–8	–24
		–6	–54
		–4	–24
		–2	–14
	n = 54		Σdp= –200

 

M = 76 +	–200	= 76–3,7 = 72,3 (ударов в минуту)

 

Среднюю арифметическую можно также рассчитать и по данным середины группы. С учетом интервала между группами. Расчет проводим по формуле:

где i — интервал между группами.

Порядок вычисления представлен в табл. (за условную среднюю принимаем М_о = 73 ударам в минуту, где i = 3)

Определение средней арифметической способом моментов

 

частота пульса V	середина группы	частота Р	условное отклонение в интерва­лах (d)	произведение условного отклонения на частоту (dp)
60–62			–4	–12
63–65			–3	–9
66–68			–2	–12
69–71			–1	–9
72–74
75–77
78–80
n = 54	Σ dp = –13

 

M = 73 +	–13х3	= 73–0,7 = 72,3 (ударов в минуту)

Таким образом, полученное значение средней арифметической величины по способу моментов идентично таковому, найденному обычным способом.