
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 7 дисперсионный анализСодержание книги
Поиск на нашем сайте Существенным недостатком лимита и амплитуды как критериев вариабельности является то, что они полностью зависят от крайних значений признака в вариационном ряду. При этом не учитываются колебания значений признака внутри ряда. Наиболее просто определить однородность числового ряда с учетом всех значений, составляющих этот ряд, через отклонения всех вариант от центра ряда (среднего арифметического), поскольку каждое отдельное наблюдение на какую-то величину не совпадает со средним арифметическим. Разность между конкретной вариантой и средним арифметическим из этого ряда называется отклонением от среднего di=(Vi – M). Такие отклонения от среднего (М=10) можно представить в графической форме:
Для получения обобщающей характеристики числового ряда использовать сумму отклонений от среднего нельзя. Это связано с тем, что сумма всех отрицательных и положительных отклонений от среднего всегда равна нулю. Можно избежать взаимной компенсации отклонений, беря квадраты отклонений, т. к. при возведении в квадрат отрицательные и положительные числа дают только положительные значения. При усреднении всех отклонений числового ряда получается средний квадрат отклонений, который называется дисперсией — D. Алгебраическое выражение дисперсии: Способы вычисления дисперсии
Упрощенные способы расчета дисперсии позволяют избежать вычислений отклонений d. В этом случае, для не сгруппированного ряда
Формула для расчета общей дисперсии представлена выражением Dобщ=Dвнгр+Dмежгр, где: Dобщ, — общая дисперсия, дисперсия значений признака всей совокупности относительно общего среднего; Dвнгр — внутригрупповая дисперсия, среднее арифметическое групповых дисперсий, взвешенных по объемам групп
группы j; Dj — дисперсия группы j; Dмежгр — межгрупповая дисперсия.
Практически расчет общей дисперсии не представляет труда. Например: требуется найти общую дисперсию совокупности состоящей из двух групп. Вычисления проходят по следующим этапам. 1-й этап: Вычисление средних в первой и второй группе
2-й этап. Вычисление общего среднего всей совокупности (обеих групп):
3-й этап: Вычисление групповых дисперсий
4-й этап. Рассчитываем внутригрупповую дисперсию, как среднюю групповых дисперсий 5-й этап. Определяем межгрупповую дисперсию, как дисперсию групповых средних относительно общего среднего:
6-й этап. Общая дисперсия Dобщ = Dвнгр +Dмежгр = 1+2,07=3,07.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 937; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 где n — число наблюдений, d — отклонения вариант от среднего di=(Vi – M). Во взвешенном ряду, дисперсия вычисляется по формуле:
где n — число наблюдений, d — отклонения вариант от среднего di=(Vi – M). Во взвешенном ряду, дисперсия вычисляется по формуле: 
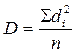

 или
или 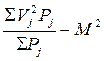
 , где ΣVj2 — сумма квадратов вариант ряда, М2 — квадрат среднего арифметического, n — число наблюдений. Для сгруппированного ряда формула вычисления дисперсии упрощенным способом выглядит следующим образом:
, где ΣVj2 — сумма квадратов вариант ряда, М2 — квадрат среднего арифметического, n — число наблюдений. Для сгруппированного ряда формула вычисления дисперсии упрощенным способом выглядит следующим образом: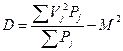 , где ΣVj2P — сумма произведений квадратов вариант ряда на их частоту, М2 — квадрат среднего арифметического, ΣPj — число наблюдений, определяемое как сумма частот. Если в результате статистического наблюдения получены несколько групп значений признака, то для вычисления обшей дисперсии можно группы в единую совокупность не объединять. Более того, если совокупность имеет большое число наблюдений (большой объем), то в случае «ручного» проведения вычислений целесообразно ее разбить на несколько групп. В том и другом случаях вычислением дисперсий отдельных групп можно заменить непосредственное вычисление общей дисперсии. Поскольку общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий. Это свойство дисперсий имеет большое теоретическое и практическое значение, являясь основой широко применяющегося в научных исследованиях дисперсионного анализа.
, где ΣVj2P — сумма произведений квадратов вариант ряда на их частоту, М2 — квадрат среднего арифметического, ΣPj — число наблюдений, определяемое как сумма частот. Если в результате статистического наблюдения получены несколько групп значений признака, то для вычисления обшей дисперсии можно группы в единую совокупность не объединять. Более того, если совокупность имеет большое число наблюдений (большой объем), то в случае «ручного» проведения вычислений целесообразно ее разбить на несколько групп. В том и другом случаях вычислением дисперсий отдельных групп можно заменить непосредственное вычисление общей дисперсии. Поскольку общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий. Это свойство дисперсий имеет большое теоретическое и практическое значение, являясь основой широко применяющегося в научных исследованиях дисперсионного анализа.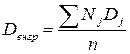 где n – объем всей совокупности, Nj — объем
где n – объем всей совокупности, Nj — объем ,где Mj — групповое среднее группы у, М — общее среднее; n — объем всей совокупности, Nj — объем группы.
,где Mj — групповое среднее группы у, М — общее среднее; n — объем всей совокупности, Nj — объем группы.





