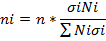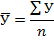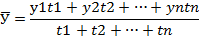Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод статистических группировок и таблиц.Содержание книги
Поиск на нашем сайте
Лекция №1 06.09.20011 Статистика – общественная наука, изучающая количественную сторону качественно определенных массовых социально-экономических явлений и процессов их структуру и распределение, размещение в пространстве, движение во времени в конкретных условиях места и времени. Статистическая методология - система приемов, способов и методов, направленных на изучение количественных закономерностей, проявляющихся в структуре, динамике и взаимосвязях социально-экономических явлений. Статистическое явление состоит из стадий: 1. Статистическое наблюдение (СН) – научно организованный сбор сведений об изучаемом социально-экономическом явлении или процессе. Метод на этой стадии – метод массовых наблюдений. Формируется Цель наблюдения: получение достоверной информации об изучаемом явлении для выявления закономерностей его развития. После определения цели выбирается объект наблюдения - некоторая статистическая совокупность, в которой протекают исследуемые социально-экономические процессы или явления, состоит из единиц наблюдения - составной элемент объекта, являющийся носителем признаков, подлежащих регистрации, состоит из отчетных единиц – субъект от которого поступают данные о единицах наблюдения. так же разрабатывают программу наблюдения - перечень признаков и вопросов, подлежащих регистрации в процессе наблюдения. Требования к программе: 1) программа должна содержать существенные признаки, непосредственно характеризующие изучаемое явление. 2) Вопросы программы должны быть точными и не двусмысленными для понимания. 3) При составлении программы необходимо определять не только круг вопросов, но и их последовательность. 4) Целесообразно включать в программу вопросы контрольного характера. 5) Вопросы программы могут быть открытыми и закрытыми. 6) Для обеспечения единообразия получаемых сведений программа оформляется в виде статистического формуляра - документ единого образца, содержащий программу и результаты наблюдений.(имеет 2 части: адресная часть-адрес отчетной единицы и ее подчиненность; титульная часть-наименование статистического наблюдения, наименование органа, проводящего это наблюдение, информацию о том кто и когда утвердил этот формуляр иногда номер, формуляр и инструкция по его исполнению составляют инструментарий статистического наблюдения) место наблюдения зависит от цели, а выбор времени состоит в решении 2 вопросов:
1) установление критического момента (даты) интервалы времени, 2) определение срока (периода) наблюдения. 2. Первичная обработка, сводка и группировка результатов наблюдения. Метод статистических группировок и таблиц. Сводка – комплекс последовательных операций по обобщению конкретных единичных фактов, образующих совокупность для выявления типичных черт и закономерностей присущих изучаемому явлению в целом. По глубине обработки сводки бывают простые и сложные; по форме обработки материала: централизованные и децентрализованные. Группировка - расчленение множества единиц, изучаемой совокупности на группы по определенным существенным для них признакам. Задачи решаемые с помощью группировок: 1) выделение социально-экономических типов явлений; 2) изучение структуры явления и структурным сдвигом происходящим в нем 3) выявление связей и взаимосвязей между явлениями 3. анализ полученных сводных материалов. Методы анализа с помощью обобщающих статист показателей
Основные организационные формы, способы и виды наблюдения Формы СН: 1. Отчетность; 2. Специально организованное наблюдение; 3. Регистры - система, постоянно следящая за единицей наблюдения и оценивающая силу воздействия различных факторов на нее. Регистры населения – поименованный список населения Регистры предприятий – аналогично Способы СН: 1. Непосредственное наблюдение 2. Документальный 3. Опрос Виды СН: 1. По времени регистрации фактов: а) единовременное наблюдение б) текущее наблюдение в) периодическая 2. По степени охвата единиц совокупности: а) сплошное наблюдение – обследованию подлежат все единицы б) не сплошное наблюдение – обследованию подлежит часть: - выборочное (единицы выбираются наугад) - метод основного массива (наиболее крупные и существенные единицы) - монографическое обследование (единицы, обычно представители новых типов чего-либо) ТОЧНОСТЬ НАБЛЮДЕНИЯ Степень соответствия величины какого-либо показателя, определенный по материалам наблюдения действительный его величине.
Расхождения между расчетным и действительным значениями носит название «ошибка наблюдения». Меры: 1) Обеспечивают качественное обучение персонала, проводящего наблюдение. 2) Организовывают специальные проверки правильности заполнения статистического формуляра. 3) Проводят логический и арифметический контроль полученных данных после сбора информации. Ошибки: 1. Ошибки регистрации – отклонение между значением показателя, полученного в ходе статистического наблюдения и фактическим действительным его значением. - случайные (результат действия случайных факторов) - систематические (например, округление) 2. Ошибки репрезентативности – отклонения значения показателя обследованной совокупности от его величины по исходной. - случайные. Возникают если отобранная совокупность неполно воспроизводит всю совокупность в целом. - систематические. Появляются вследствие нарушения принципов отбора единиц из исходной совокупности. ВИДЫ СТАТИСТИЧЕСКИХ ГРУППИРОВОК По задачам делятся на: 1. Типологические – разделение исследуемой качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки. Пример: Группировка промышленных предприятий по формам собственности
2. Структурная – группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому-либо варьирующему признаку. Пример: группировка населения по размеру денежного дохода в сентябре 2010 года в условных единицах.
3. Аналитическая группировка – группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками (факторными и результативными). Особенности: 1) В основу группировки кладется факторный признак 2) Каждая выделенная группа характеризуется средними значениями результативного признака. Группировка количества банков по сумме активов баланса:
Лекция №2 7.09.11 РЯДЫ РАСПРЕДЕЛЕНИЯ. Ряд распределения – упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку. Существуют атрибутивные ряды распределения (построенные по качественному признаку), вариационные ряды (по количественному признаку, состоят из вариантов и частот) Варианта – конкретное значение варьирующего признака. Частоты – численность отдельных вариантов или, по-другому, каждой группы вариационного ряда. Сумма всех частот определяет объем совокупности (численность). Если частоты выражены в долях единицы или в процентах к итогу, их называют частости.
В зависимости от характера вариации признака различают ряды дискретные и интервальные. Дискретный ряд характеризует распределение единиц совокупности по дискретному признаку (распределение семей по числу комнат в отдельных квартирах). Построение интервальных вариационных рядов целесообразно при непрерывной вариации признака или если дискретная вариация в широких пределах. Графики: 1) Полигон – используется при изображении дискретных вариационных рядов. 2) Гистограмма – используется для изображения интервальных вариационных рядов. 3) Кумулята (кумулятивная кривая) – при ее построении накопленные частоты определяются путем суммирования частот по группам и показывают сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение. Если при изображении вариационных рядов в виде комуляты оси поменять местами, то полученная кривая будет называться «огива». СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ Таблица называется статистической, если она содержит сводную числовую характеристику исследуемой совокупности по одному или нескольким существенным признакам взаимосвязанной логикой экономического анализа. Подлежащим в статистической таблице является объект, который характеризуется цифрами. Обычно дается в левой части в наименовании строк. Сказуемое – образует система показателей, которыми характеризуется объект изучения (подлежащее). Обычно сказуемое формирует верхние заголовки, составляет содержание глав).
Простые таблицы не дают возможности выявить социально –экономические типы явлений, их структуру и взаимосвязи между характеризующими их признаками. Монографические таблицы характеризуют не всю совокупность единиц изучаемого объекта, а только 1 группу из него. Групповые таблицы – в них подлежащее содержит группировку единиц совокупности по одному количественному или атрибутивному признаку. Комбинационные – подлежащее содержит группировку единиц совокупности по 2 или более признакам. Виды таблиц по разработке сказуемого: -таблицы с простой разработкой -таблицы со сложной разработкой При простой разработке сказуемого показатель, определяющий его, не подразделяют на подгруппы и итоговые значения получают путем простого суммирования значений по каждому признаку. При сложной разработке предполагается деление признака, формирующего его, на подгруппы.
Пример: Распределение акций среди работников приватизированных предприятий.
Сложная разработка:
Средние величины Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условия места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности. Виды средних величин: 1) Средняя арифметическая – применяется в форме простой средней и взвешенной средней.
2) Средняя гармоническая - когда статистическая информация не содержит частот (f) по отдельным группам (х), а представлена в виде их произведения (x*f), применяется формула средней гармонической взвешенной. f*x=w
средняя гармоническая – средняя взвешенная из варьирующих обратных значений признака. Применяется когда неизвестны действительные веса, т.е. f, а известно произведение f*x. Пример
Средняя гармоническая взвешенная =7780/400=19,45 В тех случаях, когда вес каждого варианта равен единице, применяется средняя гармоническая простая. 3) Средняя геометрическая
4) Средняя квадратическая
5) Структурные средние Мода и медиана Мода (Мо) – значение случайной величины, встречающееся с наибольше вероятностью в дискретном вариационном ряду. Вариант, имеющий наибольшую частоту. В интервальных рядах распределения:
Хмо – нижняя граница модального интервала iмо – модальный интервал fмо – частота в модальном интервале fмо-1 и fмо+1 – частота в предыдущем и следующим за модельным интервалом Определяется модальный интервал по наибольшей частоте. Медиана – вариант, который находится в середине вариационного ряда. Она делит ряд на 2 равные части по числу единиц, соответственно со значением признака меньше медианы и со значением признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. Рассмотрим пример. Пусть ряд состоит из показателей зарплаты. 630, 650, 680, 690, 700, 710, 720, 730 и 750 Номер медианы для нечетного объема = (n+1)/2 n-число единиц ряда В случае четного объема, медиана равна средней из двух вариантов, находящихся в середине ряда. В интервальных рядах медианное значение оказывается в каком-то из интервалов признака x.
Хме – нижняя граница медианного интервала iме – медианный интервал сумма f, деленная на 2 – половина от общего числа наблюдений
S Ме -1 = сумма наблюдений, накопленная до начала медианного интервала fме - число наблюдений в медианном интервале Мода и медиана как правило отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот в вариационном ряду. Они являют дополнительными к средней характеристике совокупности. Выборочное наблюдение Выборочное наблюдение – несплошное наблюдение, при котором статистическому обследованию подвергаются единицы изучаемой совокупности, отобранные случайным способом. Задача выборочного наблюдения: по обследуемой части дать характеристику всей совокупности при условии соблюдения всех правил и принципов проведения статистического наблюдения. Используется выборочное наблюдение в целях уточнения и для разработки данных сплошного наблюдения. Выборочный метод позволяет получить необходимые сведения приемлемой точности, когда факторы времени и стоимости делают сплошную разработку нецелесообразной. Совокупность отобранных для обследования единиц в статистике принято называть выборочной. Совокупность единиц, из которых производят отбор, называется генеральной. Символы основных параметров генеральной и выборочной совокупности.
Средняя и предельная ошибки выборки. Виды ошибок: 1. Ошибки регистрации. Могут иметь случайный и систематический характер. Случайные ошибки обычно уравновешивают друг друга, т.к. не имеют преимущественного направления в сторону уменьшения или увеличения значений признака. Систематические ошибки направлены в одну сторону вследствие преднамеренного нарушения правил отбора. Избежать их можно при правильной организации и проведении наблюдения. 2. Ошибки репрезентативности. Возникают только в выборочном наблюдении в силу того, что выборочная совокупность неполно воспроизводит генеральную. Ошибка выборочного наблюдения – разность между величиной параметра в генеральной совокупности и его величиной, вычисленной по результатам выборочного наблюдения. Для среднего значения ошибка выборки будет определяться по формуле:
Δ – предельная ошибка выборки. Величина случайная и ей посвящено несколько теорем. 1. Теорема Чебышева. При достаточно большом числе независимых наблюдений можно с вероятностью близкой к единице утверждать, что отклонение выборочной средней (
t – критерий Стьюдента. µ - средняя ошибка выборки.
n – объем выборочной совокупности Соотношение между генеральной и выборочной дисперсией:
Т.к.
2. Теорема Ляпунова. ……………………………………………. …………………………………………. ……………………………………….. Будет стремиться к единице
Из теоремы следует, что величина расхождения между долей признака выборочной совокупности и долей признака генеральной зависит как и в расхождениях средних от средней ошибки выборки. Т.к.
Т.к. доля признака в выборочной совокупности нам неизвестна, то заменяем ее через долю того же признака генеральной совокупности, т.е. принимаем, что w=p. Тогда ошибка выборки будет находиться по формуле (9). Предельная величина разности между частостью и долей называется предельной ошибкой выборки. Зная выборочную долю признака (w) и предельную ошибку (дельта w) можно определить границы, в которых заключена генеральная доля. (10) Методы формирования выборочной совокупности. В каждом конкретном случае в зависимости от ряда условий выбирают наиболее предпочтительную систему организации отбора, которая определяется видом, методом и способом отбора. По виду различают 1. индивидуальный отбор – отбираются отдельные единицы генеральной совокупности 2. групповой отбор – отбираются отдельные группы единиц 3. комбинированный отбор – сочетание индивидуального и группового Метод отбора: определяет возможность продолжения участия отобранной единицы в дальнейшей процедуре отбора. Существуют 2 метода: 1) повторный (попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную генеральную и участвует в дальнейшей процедуре отбора) 2) неповторный (попавшая в выборку единица не возвращается в исходную совокупность, из которой происходит отбор) вносится поправка: (11) (12) Способ отбора определяет конкретный механизм (процедуру выборки единиц из генеральной совокупности): 1. Собственно случайная выборка. Отбор единиц из генеральной совокупности наугад (без каких-либо элементов системности). Технически собственно случайный отбор проводят методом жеребьевки или по таблице случайных чисел. Может быть как повторным, так и бесповторным. (13) и (12) 2. Механическая выборка. Применяется когда генеральная совокупность каким-либо образом упорядочена. Для определения средней ошибки механической выборки используется формула средней ошибки как при собственно случайном бесповторном отборе. (12) 3. Серийный отбор (гнездовой). Удобен, когда единицы совокупности объединены в небольшие группы или серии. Т.к. внутри групп или серий обследуются все единицы, то средняя ошибка серийной выборки µ зависит от величины только межгрупповой дисперсии. Так определяется средняя величина ошибки для повторного. (14) (15) (16) для бесповторного 4. Типический. Используется когда все единицы генеральной совокупности можно разбить на несколько типических групп. Такой отбор может быть организован, либо пропорционален объему типических групп, либо пропорционален внутригрупповой дифференциации признака.
При выборке пропорциональной объему типических групп число единиц, подлежащих отбору из каждой группы определяется по формуле:
Ni – объем i-той группы ni – объем выборки i-той группы
При выборке пропорциональной дифференциации признака число наблюдений по каждой группе определяется:
σi – среднее квадратическое отклонение i-й группы.
Комбинированный способ отбора. Можно комбинировать циклическую выборку и серийную когда серии отбираются в установленном порядке из нескольких типических групп. Серийный и собственно случайный отбор. Когда отдельные единицы отбираются внутри серии в собственно случайном порядке. Ошибка такой выборки определяется ступенчатостью отбора. Многоступенчатый отбор. Из генеральной совокупности сначала извлекаются укрупненные группы, затем более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию. РЯДЫ ДИНАМИКИ Ряд динамики представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующего изменение общественных явлений во времени. 2 основных элемента: - время (t) – моменты или периоды, к которым относятся уровни ряда. - конкретное значение показателя (уровень ряда) (у) – показатели, числовые значения которых составляют динамический ряд. По времени, отраженному в динамических рядах, они разделяются на моментные и интервальные. Моментным рядом динамики называется такой ряд, уровни которого характеризуют состояние явления на определенные даты (на моменты времени). Интервальным (периодическим) называют такой ряд, уровни которого характеризуют разбег явления за конкретный период времени. Значения уровней интервального ряда в отличии от моментных не содержатся в последующих и предыдущих показателях. Их можно просуммировать, что позволяет получать ряды динамики более укрупненных периодов. Интервальный ряд, где последовательные уровни могут суммироваться, можно представить как ряд с нарастающими итогами. Уровни в динамическом ряду могут быть представлены абсолютными, средними или относительными величинами. По расстоянию между уровнями ряды динамики подразделяются на ряды с равностоящими и неравностоящими уровнями по времени. Если в рядах динамики прерывающиеся или неравномерные интервалы времени, то такие ряды являются неравностоящими. Ряды динамики могут быть изображены графически. Графическое изображение позволяет наглядно представить развитие явления во времени и способствует проведению анализа уровней. Правило построения рядов динамики. Статистические данные должны быть сопоставимы: 1. По территории (предполагаются одни и те же границы территории) 2. По кругу охватываемых объектов (сравнение совокупностей с равным числом элементов) При этом нужно иметь в виду, что сопоставимые показатели ряда должны быть однородны по экономическому содержанию и границам объекта, который они характеризуют. 3. По времени регистрации a. Для интервальных рядов обеспечивается равенством периодов времени, за которые приводятся данные b. Для моментных рядов показатели следует приводить на одну и ту же дату. 4. По ценам. При приведении к сопоставимому виду продукции, измеренной в стоимостных показателях трудность заключается в том, что во-первых с течением времени происходит непрерывное изменение цен и во-вторых существует несколько видов цен. Для характеристики изменения объема продукции должно быть устранено влияние изменения цен. На практике количество продукции, произведенное в разные периоды, оценивают в ценах одного и того же базисного периода, которые называют неизменными или сопоставимыми ценами. 5. По методологии расчета. При определении уровней необходимо использовать единую методологию расчетов. Часто статистические данные выражаются в различных единицах измерения, т.е. динамические ряды несопоставимы по единицам измерения. Эта несопоставимость может быть устранена путем обработки рядов динамики приемом, который носит название смыкание рядов динамики. Этот прием позволяет преодолеть несопоставимость данных вследствие изменения во времени круга охватываемых объектов или методологии расчета показателей. Имеются данные об объеме реализации продукции фирмы, в которую до 1996 года входило 10 предприятий, а с 1996 – 12. Необходимо получить единый ряд, который был бы пригоден для характеристики динамики объема реализации за весь рассматриваемый период.
Показатели за 1996-1999 гг. несопоставимы с показателями за 1993-1995 гг., т.к. относятся к разному количеству предприятий. Задача заключается в вычислении данных за 1993-1995 гг. в новых границах. Проведем смыкание рядов динамики. По данным 1996 года исчисляем коэффициент соотношения уровней 2х рядов. k=168/140=1,2 Умножая этот коэффициент на уровень ряда, получаем скорректированные данные за 1993-1995 год в новых границах. Смыкание рядов дает возможность устранить несопоставимость уровней и получить представление о динамике за весь период. ПОКАЗАТЕЛИ АНАЛИЗА РЯДА ДИНАМИКИ К показателям ряда динамики относятся абсолютный прирост, темп роста, темп прироста и абсолютное значение 1% прироста. Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста и средний темп прироста. Показатели анализа ряда динамики могут вычисляться на постоянной и переменной базах сравнения. При этом сравниваемый уровень называют отчетным, а уровень, с которым производится сравнение, называют базисным. Для расчета показателей на постоянной базе, уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. При этом исчисляемые показатели называют базисными. При расчете на переменной базе каждый последующий уровень сравнивается с предыдущим. Вычисленные при этом показатели носят название цепные. 1) Абсолютный прирост (сокращение). Характеризует увеличение или уменьшение уровня за определенный промежуток времени (2) Уi – уровень сравниваемого периода Уi-1 – уровень предшествующего периода У0 – уровень базисного периода Цепные и абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному. (3) Для оценки интенсивности (относительного изменения уровня динамического ряда за период) вычисляют темпы роста (снижения). Эта интенсивность оценивается отношением отчетного уровня к базисному. Показатель интенсивности, выраженный в долях единицы, называют коэффициентом роста в процентах темпа роста. Коэффициент роста (Кр) показывает во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение, если он больше 1 или какую часть уровня, с которым производится сравнение составляет сравниваемый уровень, если Кр меньше 1. (4) Темп роста – Кр*100 Между цепным и базисным Кр взаимосвязь: произведение последовательных цепных Кр равно базисному Кр за весь период. (5) Темп прироста (сокращения). Показывает на сколько % сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения. (6) Темп прироста можно получить из темпа роста, выраженного в %, если вычесть из него 100.
Абсолютное значение 1% прироста. А%
Рассчитывается по формуле средней хронологической (изменяется со временем). Для интервальных рядов динамики из абсолютных уровней средний уровень за период времени определяется по формуле средней арифметической. Для равных интервалов используется арифметическая простая. Для неравных – взвешенная. t-веса, или длительность интервалов времени.
С 1 по 15 число в акционерном коммерческом банке работало 20 человек. С 16 по 25 – 27 человек. С 26 по 30 – 30 человек. Посчитать среднесписочное число работников за месяц. Ответ: 24 человека. · Средний уровень моментного ряда. С равностоящими уровнями. Определяется п формуле средней хронологической моментного ряда. (2) n-число уровней у-уровни периода, за которые делается расчет. С неравностоящими уровнями: определяется по формуле средней хронологической взвешенной. (3)
Пример: масса остатков топлива в хозяйстве приведена на даты: На 1.01.09 – 40 тонн На 1.03.09 – 60 тонн На 1.04.09 – 100 тонн На 1.08.09 – 10 тонн На 1.01.10 – 30 тонн Ответ: 44,6 тонны
Обобщающий показатель скорости изменения уровней во времени является средний абсолютный прирост (убыль). Он представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний абсолютный прирост как среднюю арифметическую простую. (4) n - число абсолютных приростов в изучаемом периоде. Сравнительные характеристики направления и интенсивности роста одновременно развивающихся во времени явлений определяются приведением рядов динамики к общему основанию и расчетам коэффициентов опережения (отставания). Ряды динамики обычно приводят к одному основанию, если они не могут быть решены другими методами. По исходным уровням нескольких рядов динамики определяют относительные величины, а именно базисные темпы роста или прироста. Принятый при этом за базу сравнения период времени либо дата выступают в качестве постоянной базы расчетов темпов роста для каждого из рядов динамики. В зависимости от целей исследования базой может быть начальный, средний, либо какой-то другой уровень ряда. Сравнение интенсивности изменения уровней рядов во времени возможно с помощью коэффициента опережения. Он представляет собой отношение базисных темпов роста или прироста двух рядов динамики за одинаковые отрезки времени. Коэффициенты опережения или отставания могут быть вычислены на основе сравнения средних темпов роста или прироста. Эти коэффициенты показывают во сколько раз быстрее растет либо отстает уровень одного ряда динамики по сравнению с другим.
Динамика выпускаемой предприятием продукции в сопоставимых ценах: 2003г – 10 млрд 2004г – 13 2005г – 13 2006г – 11 2007г – 8 1) Среднегодовой выпуск продукции: (10+13+13+11+8)/5=11 2) Абсолютный прирост Δб Δц 3 3 3 0 1 -2 -2 -3 3) Коэффициент роста Кцроста 13/10 13/10 1 13/10 11/13 11/10 8/11 8/10 4) Темп прироста Цепной 30 30 0 30 -15,4 10 -27,2 -20 5) Средний темп роста – показывает во сколько раз в среднем за единицу времени изменяется уровень ряда. Является обобщенной характеристикой индивидуальных темпов роста ряда динамики.Т.к. средний темп роста представляет собой средний коэффициент роста, выраженный в %, то для равностоящих уровней расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по цепному способу). (6) Если известны уровни динамического ряда, то расчет коэффициента роста упрощается, т.к. произведение цепных коэффициентов роста равно базисному. Для равностоящих уровней расчет ведется по базисному уровню. m-число уровней ряда динамики в изучаемом периоде, включая базисный. Средние темпы прироста либо сокращения рассчитывают на основе средних темпов роста вычитанием из них 100%. Тбр Тбпр (8/10)1/4=94,6 -100 = 5,4
Остатки вкладов в Сбербанке на начало месяца:
Среднемесячные остатки: По средней хронологической. Для 1 - 7 Для 2 – 11 Методы анализа основной тенденции развития в рядах динамики. Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени свободное от случайных колебаний. Задача анализа состоит в том, чтобы выявить общую тенденцию в изменении уровне
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 404; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.162.21 (0.019 с.) |







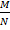

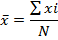
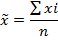
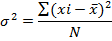
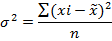
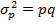
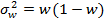
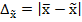
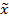 ) от генеральной средней (
) от генеральной средней (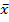 ) будет сколь угодно малой. В теореме доказано, что величина ошибки не должна превышать значение tµ. В свою очередь µ выражает отклонение выборочной средней от генеральной средней и зависит от колеблемости признака генеральной совокупности, от среднеквадратического отклонения и от числа отобранных единиц.
) будет сколь угодно малой. В теореме доказано, что величина ошибки не должна превышать значение tµ. В свою очередь µ выражает отклонение выборочной средней от генеральной средней и зависит от колеблемости признака генеральной совокупности, от среднеквадратического отклонения и от числа отобранных единиц.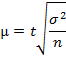
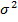 – генеральная дисперсия
– генеральная дисперсия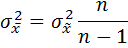
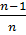 при достаточно больших n близка к единице, то принято считать, что генеральная дисперсия приблизительно равна выборочной. Из этого следует, что µ показывает какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности.
при достаточно больших n близка к единице, то принято считать, что генеральная дисперсия приблизительно равна выборочной. Из этого следует, что µ показывает какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности.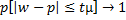
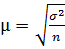 , а среднее квадратическое отклонение для доли альтернативного признака
, а среднее квадратическое отклонение для доли альтернативного признака 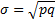 , где q=1-p, то средняя ошибка выборки для альтернативного признака будет находиться по формуле:
, где q=1-p, то средняя ошибка выборки для альтернативного признака будет находиться по формуле: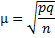
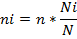
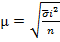 для повторного
для повторного