
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический способ изображения статистических данныхСодержание книги
Поиск на нашем сайте
Статистический график – чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью геометрических образов или знаков. Требования при построении графического изображения: 1) График должен быть достаточно наглядным (наглядно отображать статистические показатели) 2) График должен быть выразительным, доходчивым и понятным. Основные элементы графика: 1. Графический образ 2. Поле графика 3. Пространственные ориентиры 4. Экспликация графика Классификация основана на признаках: 1. Способ построения графического образа 2. Геометрические знаки, изображающие статистические показатели 3. Задачи, решаемые с помощью графического изображения По форме графического образа: 1) Линейные 2) Плоскостные 3) Объемные По способу построения: 1) Диаграммы a. Сравнения (чаще всего) b. Динамики c. Структурные 2) Статистические карты a. Картограммы b. Картодиаграммы Статистические карты – представляют собой вид графических изображений статистических данных на схематической географической карте, характеризующих уровень или степень распространения того или иного явления (процесса) на определенной территории. Средствами изображения является: штриховка, фоновая раскраска или геометрические фигуры. Картограмма – схематическая географическая карта, на которой штриховкой различной густоты либо точками или окраской определенной насыщенности показывается интенсивность какого-либо показателя в пределах каждой единицы нанесенного на карту территориального деления. Бывают они фоновые (штриховка или окраска),точечная (с помощью точек). Картодиаграмма – сочетание диаграмм с географической картой. В качестве знаков используются диаграммные фигуры (столбики, круги), размещенные на контуре географической карты. Лекция №4 Показатели вариации и анализ частотных распределений. Вариация – многообразие, колеблемость, изменяемость величины признака у единиц совокупности. Существуют вариации в пространстве и во времени. Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям. Вариации во времени – изменение значений признака в различные периоды или моменты времени. Наличие вариации признаков изучаемых явлений ставит перед статистикой задачу ее исследования, а именно: 1) Определение меры вариации 2) Ее измерение 3) Нахождение соответствующих измерителей, характеризующих ее размеры 4) Выявление их сущности и методов вычисления факторов ее определяющих. Показатели вариации делятся на 2 вида: 1) Абсолютные 1. Размах вариации R=x max – x min 2. 3. 4. Среднее линейное отклонение 2) Относительные 1. Vσ= 2. Линейный коэффициент вариации 3. ПРИМЕР: Распределение промышленных предприятий одного из регионов России по вооруженности работников промышленно-производственными ОФ. Нужно рассчитать среднее линейное отклонение.
1) Находим середины интервалов (2) по исходным данным графы (А). 2) Определяем произведение значений середины интервалов на соответствие их … записываем их в графу 3.
3) Для расчета 4) Вычисляем произведение отклонений (4) на их ……, подсчитываем сумму этих произведений и записываем в графу (5). Подсчитываем их сумму.
Ответ: 4,7. Вывод – это отклонение по сравнению со средней величиной признака очень большое. Оно отличается от средней
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 115; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.17.137 (0.01 с.) |

 Если взвешенная, то
Если взвешенная, то  . (ДИСПЕРСИЯ)
. (ДИСПЕРСИЯ) – среднее квадратическое отклонение
– среднее квадратическое отклонение
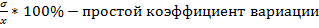
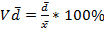





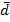 находим абсолютное отклонение середины интервалов, принятых нами в качестве вариантов признака от найденной средней величины и записываем в (4).
находим абсолютное отклонение середины интервалов, принятых нами в качестве вариантов признака от найденной средней величины и записываем в (4).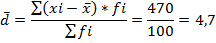
 на 2 единицы. Это свидетельствует о том, что данная совокупность в отношении нашего признака неоднородна.
на 2 единицы. Это свидетельствует о том, что данная совокупность в отношении нашего признака неоднородна.


