
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ранговые коэффициенты корреляцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ранговые коэффициенты корреляции основаны на корреляции не самих значений признаков, а их рангов. В статистике используются коэффициенты ранговой корреляции Спирмэна и Кендэла. Допустим, что объекты генеральной совокупности обладают двумя признаками, которые позволяют сравнивать объекты между собой и располагать их в порядке убывания или возрастания значения признака. Рангом называется порядковый номер объекта в ранжированном ряду. Оба признака необходимо ранжировать, то есть нумеровать в одном и том же порядке: по возрастанию или по убыванию. Если в ряду встречается несколько одинаковых значений x, то каждому из них присваивается ранг, равный частному от деления суммы рангов, приходящихся на эти значения, на число равных значений. Ранги признаков x и y обозначаются Nx и Ny. Суждение о связи между изменениями значений x и y основано на сравнении поведения рангов. Если у каждой пары x и y ранги совпадают, это характеризует максимально тесную прямую связь. Если же в одном ряду ранги возрастают от 1 до n, а в другом убывают от n до 1, то между признаками существует максимально возможная обратная связь. Для каждой пары значений признаков x и y вычислим разность их рангов Ранговой коэффициент корреляции Спирмэна вычисляется по формуле
Эту формулу можно получить из формулы для коэффициента корреляции, если вместо x и y подставить их ранги. Если ранги обоих признаков совпадают, то есть все Если ранги признаков имеют строго противоположные направления, т. е. Первому рангу x соответствует n-й (последний) ранг y, второму рангу x соответствует
Отсюда получаем
Раскрывая скобки и группирую члены суммы, получим
Методом математической индукции можно доказать, что
Тогда
следовательно, Таким образом, ранговый коэффициент корреляции Спирмэна лежит в диапазоне
Поскольку ранговый коэффициент корреляции Спирмэна учитывает только разности рангов, а не сами значения x и y, он менее точен, чем коэффициент корреляции. Поэтому при Пример. Имеется выборка из 8 заводов, каждый из которых почасовой оплатой труда x и текучестью кадров y. Результаты расчета рангового коэффициента корреляции Спирмэна приведены в таблице. Таблица 10
В данном примере ранговый коэффициент корреляции Спирмэна равен
Такое значение r говорит о сильной обратной связи между x и y.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 и квадрат разности
и квадрат разности  .
.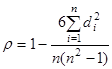 .
. и
и  . Это означает, что между признаками имеется тесная прямая связь.
. Это означает, что между признаками имеется тесная прямая связь. и т. д. то
и т. д. то  будет принимать значения
будет принимать значения ,
, 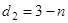 , …,
, …,  .
.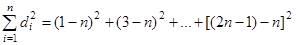 .
. .
. ,
, .
. ,
, . Это означает, что между признаками имеется максимально тесная обратная связь.
. Это означает, что между признаками имеется максимально тесная обратная связь. .
.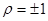 нельзя утверждать, что между x и y имеется функциональная связь. Во всех случаях, когда r не принимает крайних значений, он довольно близок к коэффициенту корреляции r.
нельзя утверждать, что между x и y имеется функциональная связь. Во всех случаях, когда r не принимает крайних значений, он довольно близок к коэффициенту корреляции r.
 .
.


