
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели тесноты связи между двумя количественными признакамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теснота связи между признаками x и y может быть измерена на основе корреляционной таблицы с помощью эмпирического корреляционного отношения
или коэффициент детерминации
где
Для характеристики связи между двумя признаками используется корреляционный момент. Корреляционным моментом называется среднее значения произведения отклонений значений признаков от их средних значений
Корреляционный момент характеризует не только зависимость величин, но и их рассеяние. Если один признак весьма мало отклоняется от своего среднего значения, то есть почти не случаен, то корреляционный момент будет мал, даже при тесной связи между признаками. Поэтому, чтобы исключить влияние рассеяния, для характеристики связи между параметрами x и y используют безразмерную величину – к оэффициент корреляции
или
Можно показать, что значения коэффициента корреляции заключены в пределах
Коэффициент корреляции характеризует не всякую зависимость, а только линейную, то есть степень тесноты линейной зависимости между параметрами. При линейной зависимости при возрастании одного параметра другой имеет тенденцию к возрастанию или убыванию по линейному закону. При Если между параметрами x и y имеется функциональная зависимость
Поскольку коэффициент корреляции вычисляется по ограниченной выборке, то он содержит случайную ошибку и не всегда отражает реальную связь между параметрами. Для того, чтобы оценить существенность (значимость) rxy и, следовательно, реальность связи между x и y, необходимо рассчитать среднюю ошибку коэффициента корреляции Если число наблюдений достаточно велико (n > 30) и есть основания полагать, что выборка извлечена из совокупности, имеющей нормальное распределение, то
Если Если задать вероятность P предельной ошибки вычисления коэффициента корреляции r, то по таблице функции F (t) можно найти коэффициент доверия. Это позволяет утверждать, что с вероятностью P истинное значение коэффициента корреляции находится в пределах
Наряду с линейным коэффициентом корреляции для измерения тесноты связи между двумя признаками используются знаковые и ранговые коэффициенты корреляции.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.83.180 (0.009 с.) |



 – межгрупповая дисперсия результативного признака y;
– межгрупповая дисперсия результативного признака y; – общая дисперсия признака y.
– общая дисперсия признака y. .
.
 .
. .
. при возрастании одного параметра другой имеет тенденцию к возрастанию (рис. 11). При
при возрастании одного параметра другой имеет тенденцию к возрастанию (рис. 11). При  при возрастании одного параметра другой имеет тенденцию к убыванию (рис. 12).
при возрастании одного параметра другой имеет тенденцию к убыванию (рис. 12). , то
, то  . Если
. Если  , это означает отсутствие линейной зависимости между параметрами. Чем ближе значение rxy к 1, тем ближе связь к функциональной.
, это означает отсутствие линейной зависимости между параметрами. Чем ближе значение rxy к 1, тем ближе связь к функциональной.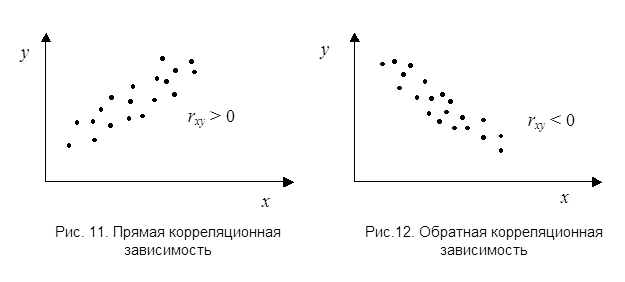
 .
. .
. , то коэффициент корреляции считается значимым, а связь – реальной.
, то коэффициент корреляции считается значимым, а связь – реальной. .
.


