
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Межгрупповая и внутригрупповая дисперсияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть имеется совокупность из n единиц, разбитая на k групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти для нее групповую среднюю и дисперсию значений признака относительно групповой средней. Часто при объединении групп требуется найти дисперсию признака всей совокупности на основе дисперсий признака в группах. При этом необходимо учитывать, что вариация признака в целом по совокупности зависит как от вариации признака внутри каждой группы, так и от вариации групповых средних. Групповой дисперсией называется дисперсия значений признака внутри группы
где ni – частота значений xi; j – номер группы;
Nj – численность j -й группы. Пример. Найти групповые дисперсии совокупности, состоящей из двух групп. Первая группа Вторая группа
N 1 = 10 N 2 = 5 Найдем групповые средние
Найдем групповые дисперсии
Зная дисперсию каждой группы, можно найти их среднюю арифметическую. Внутригрупповой дисперсией называется средняя арифметическая взвешенная групповых дисперсий
где n – общая численность всей совокупности:
Пример. Найти внутригрупповую дисперсию по данным примера 1.
Зная групповые средние и общую среднюю, можно найти дисперсию (разброс) групповых средних относительно общей средней.
где Nj – численность j -й группы;
n – численность всей совокупности. Пример. Найти межгрупповую дисперсию по данным примера 1. Найдем общую среднюю
Используя вычисленные значения
Общей дисперсией называется дисперсия значений признака всей совокупности относительно общей средней
где ni – частота значения xi;
n – численность всей совокупности. Пример. Найти общую дисперсию по данным примера 1. Учитывая, что общая средняя равна 4,67, получим
Найденная общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсии
Такая закономерность справедлива для любой совокупности. Правило сложения дисперсий (без доказательства) Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий
Это правило имеет важное практическое значение. Если в результате наблюдений получено несколько групп значений признака, то для вычисления общей дисперсии можно группы не объединять в единую совокупность. С другой стороны, если совокупность имеет большой объем, то целесообразно разбить ее на несколько групп. В обоих случаях применение правила сложения дисперсий облегчает расчеты. Коэффициентом детерминации называется отношение
Коэффициент детерминации показывает, какая доля в общей дисперсии приходится на межгрупповую дисперсию, обусловленную вариацией признака, положенного в основу группировки. Величина
называется эмпирическим корреляционным отношением. Эмпирическое корреляционное отношение показывает, насколько тесно связаны исследуемое явление и группировочный признак. Если связь отсутствует, то все групповые средние равны между собой и межгрупповой вариации нет, т.е. Если связь функциональная, то дисперсия групповых средних равна общей дисперсии Показатели дифференциации Квантилями называются значения признака, которые делят ранжированный вариационный ряд на равные по численности части. Частным случаем квантилей являются квартили, квинтили и децили. Квартилями называются значения признака, которые делят ранжированный вариационный ряд на четыре равные части. Имеются три квартили Q 1, Q 2, Q 3. Ниже первой квартили лежит ¼ часть всех значений признака, ¼ часть лежит между Q 1, и Q 2, и ¼ лежит выше Q 3. Вторая квартиль Q 2 делит вариационный ряд пополам и совпадает с медианой. Q 1 называется нижней квартилью и Q 3 – верхней. Квинтилями называются значения признака, которые делят вариационный ряд на пять равных частей. Децилями называются значения признака, которые делят вариационный ряд на десять равных частей. Децильным коэффициентом называется отношение девятой децили к первой.
Сравнивая девятую и первую дециль, измеряют соотношение уровней доходов 10% наиболее обеспеченного и 10% наименее обеспеченного населения. Моменты распределения Моментом k-го порядка называют среднее значение k-й степеней отклонения значений параметра x от некоторой постоянной величины A
При
При
при
Таким образом, начальный момент первого порядка равен средней арифметической. При
Таким образом, начальный момент второго порядка есть средний квадрат. Практически используются моменты первых четырех порядков. Если
С их помощью упрощается вычисление основных характеристик. При
при
Из этого выражения следует, что
то есть средняя арифметическая равна условному моменту первого порядка плюс начало отсчета. Если отклонения Вычисление среднего значения методом отсчета от условного нуля называется методом моментов. Практически начальные моменты относительно x0 определяют следующим образом: - из всех вариантов вычитают начало отсчета и находят отклонения - делят эти отклонения на общий множитель:
- вычисляют начальные моменты относительно x'; - умножают найденные начальные моменты на c. Результатом таких вычислений являются начальные моменты относительно x0. Если за постоянную величину A принять среднее значение, т.е.
Центральный момент нулевого порядка равен 1:
Центральный момент первого порядка равен 0:
Центральный момент второго порядка равен дисперсии:
Центральный момент третьего порядка равен
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.50.169 (0.011 с.) |

 ,
,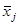 – групповая средняя j -й группы;
– групповая средняя j -й группы;



 ,
,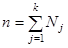 .
.

 – общая средняя;
– общая средняя;
 ,
,  , найдем межгрупповую дисперсию
, найдем межгрупповую дисперсию
 ,
,


 .
.
 , и, следовательно,
, и, следовательно,  . Это означает, что группировочный признак не влияет на вариацию исследуемого признака.
. Это означает, что группировочный признак не влияет на вариацию исследуемого признака. и отсутствует внутригрупповая вариация, и, следовательно,
и отсутствует внутригрупповая вариация, и, следовательно,  . Это означает, что группировочный признак полностью определяет вариацию исследуемого признака. Таким образом,
. Это означает, что группировочный признак полностью определяет вариацию исследуемого признака. Таким образом,  .
. .
. момент называется начальным:
момент называется начальным: .
. получаем начальный момент нулевого порядка
получаем начальный момент нулевого порядка ,
, – начальный момент первого порядка
– начальный момент первого порядка .
. получаем начальный момент второго порядка
получаем начальный момент второго порядка .
. , то моменты называются начальными относительно x0 или условными (x0 играет роль начала отсчета):
, то моменты называются начальными относительно x0 или условными (x0 играет роль начала отсчета): .
. ,
, .
. ,
, имеют общий множитель c, то на него можно разделить отклонения, а после окончания вычислений полученный момент умножить на этот множитель.
имеют общий множитель c, то на него можно разделить отклонения, а после окончания вычислений полученный момент умножить на этот множитель. ;
; , то моменты называются центральными и обозначаются mk:
, то моменты называются центральными и обозначаются mk: .
. .
. .
. .
. .
.


