
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7. Экономические индексыСодержание книги
Поиск на нашем сайте
Понятие индекса Индексом называется относительный показатель, характеризующий соотношение значений какого-либо параметра во времени, в пространстве или по сравнению с планом. Показатель, изменение которого характеризуется индексом, называется индексируемой величиной. Она содержится в названии индекса, например индекс цен, индекс физического объема продукции. Обычно используются следующие обозначения: q – количество товара (продукции) в натуральном выражении; p – цена единицы товара; c – себестоимость единицы продукции; t – затраты времени на производство единицы продукции (трудоемкость). Величины, соответствующие базисному периоду (базе сравнения), обозначаются значком 0, отчетному (текущему) периоду – 1. По степени охвата единиц совокупности индексы делятся на индивидуальные и общие (сводные). Индивидуальные индексы характеризуют относительное изменение отдельного элемента совокупности, например, изменение цены на молоко, изменение объема добычи нефти. Например:
Индивидуальные индексы показывают во сколько раз увеличилась (уменьшилась) индексируемая величина по сравнению с базовым периодом. В экономике часто возникает необходимость расчета сводных показателей для совокупности, элементы которой несопоставимы. Например, нельзя суммировать тонны нефти с метрами ткани. Общие (сводные) индексы характеризуют относительное изменение индексируемой величины в совокупности, отдельные элементы которой несоизмеримы. Общие индексы могут быть построены как агрегатные или как средние из индивидуальных. Агрегатные индексы Построение агрегатного индекса сводится к тому, что с помощью определенных соизмерителей вычисляется итоговая величина для всей совокупности в отчетном и базовом периодах, а затем первая сопоставляется со второй. Чаще всего в качестве соизмерителя выступает цена единицы продукции. Умножая цены на количество произведенной продукции, получаем стоимостное выражение продукции каждого вида, которое допускает суммирование. Общие индекс, полученный путем сопоставления итоговых показателей в отчетном и базисном периодах, выраженных с помощью соизмерителя, называется агрегатным. Чтобы изменение цен влияло на величину общей стоимости продукции, продукцию двух лет надо оценивать в одних и тех же ценах. В этом случае стоимость продукции двух периодов будет отличаться лишь за счет изменения объема продукции. Общий индекс, вычисленный как отношение стоимости продукции двух периодов в ценах базисного года, называется агрегатным индексом физического объема
где В качестве соизмерителя могут выступать также себестоимость единицы продукции или затраты на производство единицы продукции. По аналогии с индексом физического объема может быть построен агрегатный индекс цен. Пусть необходимо устранить влияние изменения количества произведенной продукции в разные периоды на ее общую стоимость. Для этого один и тот же количественный набор товаров надо выразить в ценах отчетного и базисного периодов. Если количественный набор фиксируется на уровне базисного периода, получаем агрегатный индекс цен Ласпейраса
Если количественный набор фиксируется на уровне текущего года, получаем агрегатный индекс цен Пааше
Средние индексы Общие индексы могут быть вычислены не только как агрегатные, но и как средние из индивидуальных. Оба метода дают одинаковый результат. Средние индексы вычисляются в форме среднего арифметического и среднего гармонического индивидуальных индексов. Для любого k-го продукта индивидуальный индекс объема
Отсюда продукция отчетного периода k-го вида
Подставляя это выражение в формулу для агрегатного индекса физического объема, получаем средний арифметический индекс физического объема
Аналогично, выражая продукцию базисного периода в виде
и подставляя в формулу для агрегатного индекса физического объема, получаем средний гармонический индекс физического объема
Применительно к индексам цен возможны два варианта усреднения, в зависимости от того, по отношению к какому агрегатному индексу оно относится: к индексу Ласпейраса или индексу Пааше. Если за исходную принимается формула Ласпейраса, то, подставляя в числитель
Здесь весами при усреднении индексов служат стоимости отдельных групп продукции базисного периода в ценах базисного периода Если за исходную принять формулу Пааше, получим средний арифметический индекс цен по Пааше
В этом случае весами при усреднении служат стоимости отдельных групп продукции отчетного периода в базисных ценах Чтобы записать формулы среднего гармонического индекса цен, из выражения
выражаем цену базисного периода
и подставляем это выражение в знаменатель формулы для агрегатного индекса цен. Тогда средний гармонический индекс цен по Ласпейрасу будет иметь вид
Аналогично, средний гармонический индекс цен по по Пааше имеет вид
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.006 с.) |

 – индекс объема одного определенного товара;
– индекс объема одного определенного товара; – индекс цены определенного товара.
– индекс цены определенного товара. ,
, – объем товара k-го вида в базисном и текущем году,
– объем товара k-го вида в базисном и текущем году, 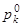 – цена товара k-го вида в базисном году.
– цена товара k-го вида в базисном году. .
. .
. .
. .
.

 .
. , получим средний арифметический индекс цен по Ласпейрасу
, получим средний арифметический индекс цен по Ласпейрасу .
. .
. .
. .
.

 ,
, .
.


