
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод укрупненных интерваловСодержание книги
Поиск на нашем сайте
Чем меньше период, за который проводятся данные, тем больше влияние случайных факторов. В ряду с укрупненными интервалами времени закономерность изменения уровней будет наглядней. Пример. Имеются данные о выпуске продукции на предприятии по месяцам. Таблица 12
Укрупним интервалы до трех месяцев и рассчитаем суммарный и среднемесячный выпуск продукции по кварталам. Таблица 13
Новые данные более четко выражают тенденцию увеличения выпуска продукции в квартала. Метод скользящего среднего По этому методу фактические уровни заменяются средними, рассчитанными для последовательных скользящих укрупненных интервалов, охватывающих m уровней (рис. 13).
Например, при Аналитическое выравнивание Каждый фактический уровень y рассматривается как сумма
где e – случайная величина, вызывающая колебания уровней вокруг тренда. Задача аналитического выравнивания состоит в - определении на основе фактических данных вида функции - нахождении параметров этой функции; - расчете по найденному уравнению теоретических (выровненных) уровней. Наиболее часто используются следующие функции - линейная: - парабола: - показательная: - гиперболическая: - ряд Фурье: Наиболее часто для нахождения параметров аналитической функции Например, при выравнивании по прямой
где n – количество членов ряда;
В случае периодических колебаний уровней ряда используется выравнивание с помощью ряда Фурье. Оно дает хорошие результаты для рядов, содержащих сезонные колебания
Периодические колебания уровней динамического ряда представляются в виде суммы m гармоник. Например, при
при
Коэффициенты ряда Фурье вычисляются по формулам
Последовательные значения t отсчитываются от 0 с шагом Измерение сезонных колебаний осуществляется с помощью индексов сезонности, которые вычисляются двумя способами. По данным ряда лет рассчитывается среднее значение уровня Индекс сезонности для каждого месяца вычисляется как процентное отношение среднего уровня данного месяца к среднему месячному уровню всего ряда
Для каждого года рассчитываются помесячные индексы сезонности, а затем для индексов одноименных месяцев находится среднее арифметическое значение.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.91.173 (0.005 с.) |


 сначала вычисляется среднее значение для первых трех уровней, затем для второго, третьего и четвертого, потом для третьего, четвертого и пятого и т.д. Это обеспечивает взаимное погашение случайных колебаний уровней. Скользящее среднее относится к середине скользящего интервала.
сначала вычисляется среднее значение для первых трех уровней, затем для второго, третьего и четвертого, потом для третьего, четвертого и пятого и т.д. Это обеспечивает взаимное погашение случайных колебаний уровней. Скользящее среднее относится к середине скользящего интервала.
 – систематическая составляющая, отражающая тренд;
– систематическая составляющая, отражающая тренд; , наиболее точно отражающих тренд;
, наиболее точно отражающих тренд; ;
; ;
; ;
; ;
; .
. и
и  определяются путем решения системы нормальных уравнений, которая получается путем замены
определяются путем решения системы нормальных уравнений, которая получается путем замены  на
на  .
.
 – уровни эмпирического ряда.
– уровни эмпирического ряда.



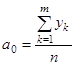 ,
,
 .
. , n – число членов ряда.
, n – число членов ряда. для каждого месяца и средний месячный уровень за весь период
для каждого месяца и средний месячный уровень за весь период 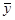 .
. .
.


