
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение необходимого объема выборкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Среднее значение признака, вычисленное по всей генеральной совокупности, называется генеральной средней и обозначается Среднее значение признака, вычисленное по выборке, называется выборочным средним и обозначается Аналогичным образом определяется генеральная дисперсия Вычисляя выборочное среднее для различных выборок одинакового объема n из одной генеральной совокупности, можно заметить, что эта величина не совпадает с генеральной средней и изменяется от выборки к выборке. Причина заключается в меньшем объеме выборки по сравнению с генеральной совокупностью Средней ошибкой выборки m называется среднее квадратическое отклонение все х возможных значений выборочной средней от генеральной средней. Средняя ошибка выборки характеризует среднюю величину возможных расхождений выборочной и генеральной средней. При случайном повторном отборе
При случайном бесповторном отборе
где N – объем генеральной совокупности; n – объем выборки. Если признак является альтернативным и w – доля единиц выборке, обладающих признаком, а Средняя ошибка отбора для доли при случайном повторном отборе
Средняя ошибка отбора для доли при случайном бесповторном отборе
При увеличении объема выборки средняя ошибка выборки уменьшается. Учитывая, что на основе выборочного обследования нельзя точно оценить изучаемый параметр генеральной совокупности, необходимо найти пределы, в которых он находится. Каждое отклонение Предельная ошибка выборки D определяется в долях средней ошибки
где t – коэффициент доверия, зависящий от вероятности P, с которой определяется предельная ошибка выборки. Вероятность P определяется по специальным таблицам, в которых она вычисляется как функция t по формуле
Задав вероятность P, можно найти коэффициент доверия t. Это позволяет утверждать, что с вероятностью P генеральная средняя находится в пределах
При Можно решить и обратную задачу: задав предельную ошибку выборки, определить вероятность, с которой она может быть гарантирована. При этом. Зная D и m, сначала находят коэффициент доверия
а затем по таблице искомое значение вероятности. При случайном повторном отборе предельная ошибка выборки равна
Отсюда можно найти необходимый объем выборки
Таким образом, для определения необходимого объема выборки должны быть заданы ее предельная ошибка и вероятность того, что эта ошибка не превысит заданного предела. В соответствии с этой вероятностью по таблице находят коэффициент доверия t. Наиболее сложно определить дисперсию изучаемого признака в генеральной совокупности. Поскольку при большом объеме выборки выборочная дисперсия близка к генеральной дисперсии, то вместо генеральной дисперсии используют выборочную дисперсию. Генеральную дисперсию можно оценить, зная коэффициент вариации по итогам предшествовавшего наблюдения
Отсюда следует, что генеральная дисперсия равна
При случайном бесповторном отборе объем выборки определяется по формуле
Если в результате выборочного обследования необходимо установить долю единиц, обладающих определенным значением альтернативного признака, то дисперсия для доли будет равна pq. В этом случае объем выборки определяется по формуле
Если доля единиц p, обладающих признаком, неизвестна, то принимают Если объем выборки
во-вторых, при нахождении вероятности допуска той или иной ошибки пользоваться таблицами распределения Стьюдента.
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 527; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.46 (0.007 с.) |

 .
. .
. и выборочная дисперсия
и выборочная дисперсия  .
. .
. ,
,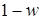 – доля единиц, не обладающих признаком, то дисперсия признака равна
– доля единиц, не обладающих признаком, то дисперсия признака равна  .
. .
. .
.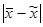 от m имеет определенную вероятность. Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной средней и установить пределы, в которых находится изучаемый параметр признак в генеральной совокупности.
от m имеет определенную вероятность. Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной средней и установить пределы, в которых находится изучаемый параметр признак в генеральной совокупности.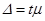 ,
, .
. .
. эта вероятность равна 0,997.
эта вероятность равна 0,997. ,
, .
. .
.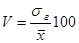 %.
%. .
. .
. .
. , при этом значение дисперсии альтернативного признака максимально.
, при этом значение дисперсии альтернативного признака максимально.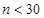 , то выборка называется малой. В этом случае необходимо, во-первых, в формуле средней ошибки в знаменателе заменить n на n- 1, т.е. вычисления проводить по формуле
, то выборка называется малой. В этом случае необходимо, во-первых, в формуле средней ошибки в знаменателе заменить n на n- 1, т.е. вычисления проводить по формуле ,
,


