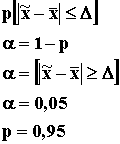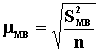Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение оптимального объема выборки. (формулы в тетради)Содержание книги
Поиск на нашем сайте
Заключительным этапом является распространение результатов выборочного обследования на генеральную совокупность. Вывод о возможности распространения зависит от полноты выборки. Под полнотой понимается наличие или представленность всех типов и групп данной генеральной совокупности в основе выборки. Более точной основой суждения о распространении результатов является расчет относительной ошибки: для средней:; для доли:. Если величина относительной ошибки не превышает заранее установленного для данного обследования предельного значения, то данные выборочного наблюдения являются представительными и могут быть распространены на генеральную совокупность. Распространение характеристик выборочной совокупности на генеральную совокупность является целью любого выборочного наблюдения. При этом исходят из того, что все средние и относительные показатели, полученные по выборке, являются несмещенными и эффективными характеристиками генеральной совокупности. Распространять эти характеристики можно с помощью различных приемов. Применение того или иного приема распространения зависит от цели выборочного исследования. Прямой пересчет данных выборки на всю совокупность применяется в том случае, когда целью исследования является определение объема признака генеральной совокупности, если известка лишь численность ее единиц. При этом способе для получения средних характеристик генеральной совокупности выборочные средние величины или доли умножаются на объем генеральной совокупности:
Учитывая предельную ошибку выборки, можно утверждать, что с определенной вероятностью характеристика генеральной совокупности находится в доверительном интервале:
Итоговый подсчет по генеральной совокупности можно получить на основе итогового подсчета по выборке, разделив его величину на долю отбора единиц совокупности:
Прежде чей производить расчет объемных показателей для генеральной совокупности, нужно убедиться, что структура выборки соответствует структуре генеральной совокупности. При наличии значительныхсмещений в структуре выборки, в долях отдельных групп, следует применить метод перевзвешивания, т. е. рассчитывать генеральную среднюю на основе выборочных средних по группам и удельного веса этих групп в генеральной совокупности:
В том случае, если выборочное наблюдение проводится с целью уточнения результатов сплошного наблюдения, применяется метод коэффициентов. Пусть по данным сплошного учета была получена величина изучаемого признака - Nген, в том числе в некоторой части генеральной совокупности – N1. Контрольное выборочное наблюдение по этой части генеральной совокупности предоставило уточненные данные – Nвыб. Тогда поправочный коэффициент:
Тогда скорректированная характеристика генеральной совокупности рассчитывается: N=N’+ В процессе статистических исследований нередко приходится ограничивать объем выборки, особенно в тех случаях, когда исследования единиц совокупности приводит к их разрушению. В статистике доказано, что даже в выборке весьма малого объема (20-30, а иногда 4-5 единиц) позволяют получить приемлемые для анализа результаты. Проблема малых выборок была решена в 1908г. английским статистиком У.Гассетом (псевдоним Студент). Он сумел определить зависимость между величиной доверительного коэффициента t, а так же численностью малой выборки n с одной стороны, и вероятностью нахождения ошибки выборки в заданных пределах с другой стороны. Эта зависимость получила название – распределение Стьюдента. Для упрощения расчетов имеются специальные таблицы значений критериев Стьюдента (стр. 372 «Практикума по теории статистики»). n=n-1 – число степеней свободы. Малая выборка определяется по формуле
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.100 (0.01 с.) |

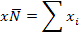

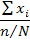
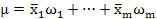 , где
, где 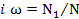
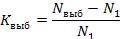
 N;
N;