
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средняя ошибка малой выборкиСодержание книги
Поиск на нашем сайте
Дисперсия малой выборки - число степеней свободы.
Пример: Ежедневные затраты времени 15 работников на поездки туда и обратно составляют в среднем 1,7 часа. Определить пределы, в которых находится среднее время поездки на работу и обратно.
n=15 S2=0,134
P=0,95 33. Основные понятия корреляционного и регрессионного анализа.Исследуя природу, общество, экономику, необходимо считаться со взаимосвязью наблюдаемых процессов и явлений. При этом полнота описания так или иначе определяется количественными характеристиками причинно-следственных связей между ними. Оценка наиболее существенных из них, а также воздействия одних факторов на другие является одной из основных задач статистики. Формы проявления взаимосвязей весьма разнообразны. В качестве двух самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции. Достаточно часто функциональная связь проявляется в физике, химии. В экономике примером может служить прямо пропорциональная зависимость между производительностью труда и увеличением производства продукции. Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции. Например, некоторое увеличение аргумента повлечет за собой лишь среднее увеличение или уменьшение (в зависимости от направленности) функции, тогда как конкретные значения у отдельных единиц наблюдения будут отличаться от среднего. Такие зависимости встречаются повсеместно. Например, в сельском хозяйстве это может быть связь между урожайностью и количеством внесенных удобрений. Очевидно, что последние участвуют в формировании урожая. Но для каждого конкретного поля, участка одно и то же количество внесенных удобрений вызовет разный прирост урожайности, так как во взаимодействии находится еще целый ряд факторов (погода, состояние почвы и др.), которые и формируют конечный результат. Однако в среднем такая связь наблюдается – увеличение массы внесенных удобрений ведет к росту урожайности.
По направлению связи бывают прямыми, когда зависимая переменная растет с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать соответственно положительными и отрицательными. Относительно своей аналитической формы связи бывают линейными и нелинейными. В первом случае между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно. Существует еще одна достаточно важная характеристика связей с точки зрения взаимодействующих факторов. Если характеризуется связь двух признаков, то ее принято называть парной. Если изучаются более чем две переменные – множественной. Указанные выше классификационные признаки наиболее часто встречаются в статистическом анализе. Но кроме перечисленных различают также непосредственные, косвенные и ложные связи. Собственно, суть каждой из них очевидна из названия. В первом случае факторы взаимодействуют между собой непосредственно. Для косвенной связи характерно участие какой-то третьей переменной, которая опосредует связь между изучаемыми признаками. Ложная связь – это связь, установленная формально и, как правило, подтвержденная только количественными оценками. Она не имеет под собой качественной основы или же бессмысленна. По силе различаются слабые и сильные связи. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей. В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – регрессионный анализ. В то же время ряд исследователей объединяет эти методы в корреляционно-регрессионный анализ, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнения при интерпретации результатов и др.
Поэтому в данном контексте можно говорить о корреляционном анализе в широком смысле – когда всесторонне характеризуется взаимосвязь. В то же время выделяют корреляционный анализ в узком смысле – когда исследуется сила связи – и регрессионный анализ, в ходе которого оцениваются ее форма и воздействие одних факторов на другие. Задачи собственно корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов оказывающих наибольшее влияние на результативный признак. Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной. Решение названных задач опирается на соответствующие приемы, алгоритмы, показатели, применение которых дает основание говорить о статистическом изучении взаимосвязей. Следует заметить, что традиционные методы корреляции и регрессии широко представлены в разного рода статистических пакетах программ для ЭВМ. Исследователю остается только правильно подготовить информацию, выбрать удовлетворяющий требованиям анализа пакет программ и быть готовым к интерпретации полученных результатов. Алгоритмов вычисления параметров связи существует множество, и в настоящее время вряд ли целесообразно проводить такой сложный вид анализа вручную. Вычислительные процедуры представляют самостоятельный интерес, но знание принципов изучения взаимосвязей, возможностей и ограничений тех или иных методов интерпретации результатов является обязательным условием исследования. Методы оценки тесноты связи подразделяются на корреляционные (параметрические) и непараметрические. Параметрические методы основаны на использовании, как правило, оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. На практике это положение чаще всего принимается априори. Собственно, эти методы – параметрические – и принято называть корреляционными. Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Их преимуществом является и простота вычислений. 34. Понятия взаимосвязанных признаков как предмет статистического изучения связи. Задачи статистического изучения связи. Виды взаимосвязей и цели их статистического изучения. Изучение причинно-следственных зависимостей между фактами – важнейшая задачаанализа социально-экономических явлений. Это необходимо для принятияобоснованных управленческих решений. Изучение зависимостей – это сложнейшаязадача, поскольку социально-экономические явления сами по себе сложны имногообразны. Кроме того, полученные выводы носят вероятностный характер, таккак они делаются на основе данных, представляющих собой выборку во времениили пространстве.Статистические методы изучения зависимости построены с учетом особенностейизучаемых закономерностей. Статистика изучает преимущественно стохастическиесвязи, когда одному значению признака-фактора соответствует группа значенийрезультативного признака. Если с изменением значений признака-фактораизменяются среднегрупповые значения результативного признака, то такие связиназывают корреляционными. Не всякая стохастическая зависимость являетсякорреляционной. Если каждому значению факторного признака соответствует строгоопределенное значение результативного признака, то такая зависимость функциональная. Ее называют еще полной корреляцией. Неоднозначныекорреляционные зависимости называют неполной корреляцией. По механизму взаимодействия различают:§ Непосредственные связи – когда причина прямо влияет на следствие;§ Косвенные связи – когда между причиной и следствиемсуществуют ряд промежуточных признаков (например, влияние возраста назаработок).По направлениям различают:§ Прямые связи – когда значение факторного ирезультативного признаков изменяются в одном направлении;§ Обратные связи – когда значения факторного ирезультативного признаков изменяются в разных направлениях.Бывают:§ Прямолинейные (линейные) связи – выражены прямой линией;§ Криволинейные связи – выражены параболой, гиперболой.По числу взаимосвязанных признаков различают:§ Парные связи – когда анализируется взаимосвязь двух признаков(факторного и результативного);§ Множественные связи – характеризуют влияние нескольких признаков наодин результативный.По силе взаимодействия различают:§ Слабые (заметные) связи; § Сильные (тесные) связи. Задача статистики определить наличие, направление, форму и тесноту взаимосвязи. 35. Выбор формы управления регрессии для анализа экономических явлений. Оценка параметров управления регрессии. Корреляционное отношение изменяется в пределах от 0 до 1, и анализ степени тесноты связи полностью соответствует линейному коэффициенту корреляции. Чем теснее связь между х и у, тем меньше, а η больше.Выбор формы уравнения регрессии: 1) Для каждой зависимости определяют корреляционное отношение (для линейной зависимости коэффициент корреляции), определяется критерий Дарбина-Уотсона и ошибка аппроксимации; 2) Из зависимостей выбирают такие, у которых отсутствует автокорреляция остатков; 3) Из оставшихся уравнений регрессии выбирают то, для которого корреляционное отношение имеет наибольшее значение (для линейной зависимости коэффициент корреляции). Если таких зависимостей несколько, то выбирается та зависимость, у которой ошибка аппроксимации имеет наименьшее значение. При этом линейной зависимости, независимо от величины ошибки аппроксимации, отдается предпочтение. Построение модели множественной регрессии включает несколько этапов: - выбор формы связи (уравнения регрессии) - отбор факторных признаков Выбор формы связи затрудняется тем, что, используя математический аппарат, теоретическая зависимость между признаками может быть выражена большим числом различных функций. Поскольку уравнение регрессии строится главным образом для объяснения и количественного отображения взаимосвязей, оно должно хорошо отражать сложившиеся между исследуемыми факторами фактические связи. Важным этапом построения уже выбранного уравнения множественной регрессии является отбор и последующее включение факторных признаков. Проблема отбора факторных признаков для построения моделей может быть решена на основе эвристических или многомерных статистических методов анализа. Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия (шаговый регрессионный анализ). Сущность метода шаговой регрессии заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости. Одновременно используется и обратный метод, т.е. исключение факторов, ставших незначимыми на основе t-критерия Стьюдента. Оценка параметров уравнения регреcсии. Пример
Задание: Требуется:
Посмотрите, как легко было найдено уравнение степенной регрессии с помощью сервиса.
Решение: 1. Уравнение имеет вид y = α + βx
Дисперсия Среднеквадратическое отклонение Коэффициент корреляции Коэффициент детерминации
Доверительный интервал для коэффициента корреляции Межгрупповая и общая дисперсии помогают определить, на сколько сильно результат педагогического эксперимента (или любого другого опыта) обусловлен принадлежностью испытуемого к той или иной группе. Для этого используетсякоэффициент детерминации Рассмотрим пример. Пусть оценки, полученные на ЕГЭ по математике выпускниками классов с разными профилями, описаны в следующей таблице.
Определим, в какой степени успешность сдачи ЕГЭ зависит от принадлежности учащегося к той или иной группе. Для этого сначала найдем средний балл за экзамен для всей совокупности испытуемых:
Найдем межгрупповую дисперсию:
Определим общую дисперсию:Dв=Dвнгр+Dмежгр=9,98+45,66=55,64. Следовательно: Полученный коэффициент детерминации показывает, что успешность сдачи ЕГЭ в данном опыте на 82% обусловлена принадлежностью учащегося к той или иной группе. Используют также эмпирическое корреляционное отношение, получаемое извлечением квадратного корня из коэффициента детерминации. В рассмотренном примере Общая дисперсия помогает численно оценить, как сильно отличаются варианты выборки друг от друга. Межгрупповая дисперсия помогает выявить степень различия между группами данной выборки. Однако, в педагогических исследованиях зачастую не требуется численная оценка параметра, но при этом важно знать, существенно ли отличаются испытуемые (или группы испытуемых) друг от друга по тому или иному признаку. Ответ на такой вопрос даёт коэффициент вариации. Расчет линейного коэффициента корреляции Пирсона: В статистической практике могут встречаться такие случаи, когда качества факторных и результативных признаков не могут быть выражены численно. Поэтому для измерения тесноты зависимости необходимо использовать другие показатели. Для этих целей используются так называемые Наибольшее распространение имеют Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены
где d = Nx - Ny, т.е. разность рангов каждой пары значений х и у; n - число наблюдений.
где S = P + Q. К непараметрическим методам исследования можно отнести Для определения этих коэффициентов создается расчетная таблица (таблица «четырех полей»), где статистическое сказуемое схематически представлено в следующем виде:
Здесь а, b, c, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков Коэффициент ассоциации можно расcчитать по формуле
Коэффициент контингенции рассчитывается по формуле
Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации. Если необходимо оценить тесноту связи между альтернативными признаками, которые могут принимать любое число вариантов значений, применяется Для исследования такого рода связи первичную статистическую информацию располагают в форме таблицы:
Здесь mij - частоты взаимного сочетания двух атрибутивных признаков; П - число пар наблюдений.
где
Коэффициент взаимной сопряженности изменяется от 0 до 1. Наконец, следует упомянуть
где na - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической; nb- соответственно количество несовпадений. Коэффициент Фехнера может изменяться в пределах -1,0 Для исследования взаимосвязи качественных альтернативных признаков, принимающих только 2 взаимоисключающих значения, используется коэффициент ассоциации и контингенции. При расчете этих коэффициентов составляется т.н. таблица 4-х камней, а сами коэффициенты рассчитываются по формуле:
Если коэффициент ассоциации ³ 0,5, а коэффициент контингенции ³ 0,3, то можно сделать вывод о наличии существенной зависимости между изучаемыми признаками. Если признаки имеют 3 или более градаций, то для изучения взаимосвязей используются коэффициенты Пирсена и Чупрова. Они рассчитываются по формулам: С - коэффициент Пирсена К - коэффициент Чупрова j - показатель взаимной сопряженности K - число значений (групп) первого признака K1 - число значений (групп) второго признака fij - частоты соответствующих клеток таблицы mi - столбцы таблицы - j - строки Для расчета коэффициентов Пирсена и Чупрова составляется вспомогательная таблица:
При ранжировании качественных признаков с целью изучения их взаимосвязи используется коэффициент корреляции Кэндалла. - - число наблюдений S - сумма разностей между числом последовательностей и числом инвервий по второму признаку. S=P+Q P - сумма значений рангов, следующих за данными и превышающих его величину Q - сумма значений рангов, следующих за данными и меньших его величины (учитывается со знаком «-»). При наличии связанных рангов формула коэффициента Кендалла будет следующей: Vxи Vyопределяются отдельно для рангов Xи Yпо формуле: Рядами динамики называются последовательно расположенные в хронологическом порядке статистические данные, отображающие развитие изучаемого явления во времени. В каждом ряду динамики имеются два основных элемента: 1. показатель времени t, который может быть представлен в виде определенных дат (моментов) времени, либо отдельных периодов (год, квартал, месяц, сутки); 2. уровни развития изучаемого явления у – отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами. В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим, ряды динамики подразделяются на: 1. моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени, например, остатки товаров на складе готовой продукции на определенный момент времени (дату); 2. интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени, например товарооборот предприятия за определенный период. Чем больше изменчивость явления во времени, тем меньше должны быть промежутки во времени между данными. Отличительной особенностью моментного и интервального рядов динамики является понятие интервала. Для моментного ряда динамики интервал – промежуток времени между датами. § полный ряд - ряд динамики, в котором одноименные моменты времени или периоды времени строго следуют один за другим в календарном порядке или равноотстоят друг от друга. § неполный ряд динамики - ряд, в котором уровни зафиксированы в неравноотстоящие моменты или периоды времени. 40. Правила построения ряда динамики.1. Периодизация развития, т.е. расчленение его во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. По существу, это типологическая группировка во времени. 2. Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета. 3. Величины временных интервалов должны соответствовать интенсивности изучаемых процессов. Чем больше вариация уровней во времени, тем чаще следует делать замеры, соответственно для стабильных процессов интервалы можно увеличить. 4. Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями. 41. Показатели анализа ряда динамикиПри изучении явления во времени перед исследователем встает проблема описания интенсивности изменения и расчета средних показателей динамики. Решается она путем построения соответствующих показателей. Для характеристики интенсивности изменения во времени такими показателями будут: Расчет показателей динамики представлен в следующей таблице.
* В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях. 42. Структура ряда динамики. Проверка ряда на наличие тренда.Всякий ряд динамики теоретически может быть представлен в виде составляющих: Ø тренд – основная тенденция развития ряда, обусловливающая увеличение или снижение его уровней; Ø циклические (периодические) колебания (в том числе сезонные); Ø случайные колебания. Проверка ряда динамики на наличие в нем тренда возможна несколькими способами (в порядке усложнения): 1. Графический метод, когда на графике по оси абсцисс откладывается время, а по оси ординат – уровни ряда. Соединив полученные точки линиями, в большинстве случаев можно выявить тренд визуально. 2. Метод средних, согласно которому изучаемый ряд динамики делится на два равных подряда, для каждого из которых определяется средняя величина 3. Метод Кокса и Стюарта, согласно которому ряд динамики делится на три равные по числу уровней группы и существенное различие выявляется между средними уровнями первой и третьей групп. Если общее число уровней не делится на три, то надо добавить недостающий уровень или исключить излишний. 4. Метод Валлиса и Мура, согласно которому наличие тренда признается в том случае, если ряд не содержит либо содержит в приемлемом количестве фазы, т.е. перемену знака при определении абсолютного изменения цепным способом. 5. Метод серий, согласно которому каждый уровень ряда считается принадлежащим к одному из двух типов, например типу А – меньше медианного или среднего значения или типу В – больше его. Затем в образовавшейся последовательности типов устанавливается число серий R. Они называются последовательностью уровней одинакового типа, которая граничит с уровнями другого типа. Если в ряду динамики общая тенденция к росту или снижению уровней отсутствует, то число серий является случайной величиной, распределенной приближенно по нормальному закону (при n>30) или по распределению Стьюдента (при n<30). Следовательно, если закономерности в изменениях уровней нет, то случайная величина R оказывается в доверительном интервале
где t – коэффициент доверия для принятого уровня вероятности при нормальном законе или со степенью свободы k = (n - 1) при распределении Стьюдента;
Подставляя среднее число серий и его среднее квадратическое отклонение в доверительный интервал, получим его развернутое значение в виде
При анализе колеблемости динамических рядов наряду с выделением случайных колебаний, возникает задача изучения периодических колебаний. Как правило, изучение периодических (сезонных) колебаний необходимо с целью исключения их влияния на общую дина
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 464; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.205.92 (0.017 с.) |



 =1,7 часа
=1,7 часа .
.
 Далее следует определить внутригрупповую дисперсию:
Далее следует определить внутригрупповую дисперсию:
 .
. . Чем ближе значение корреляционного соотношения к единице, тем более тесную связь мы наблюдаем. Соответственно, в данном случае было показано наличие тесной связи между успешностью сдачи ЕГЭ и принадлежностью учащегося к той или иной группе обучаемых.
. Чем ближе значение корреляционного соотношения к единице, тем более тесную связь мы наблюдаем. Соответственно, в данном случае было показано наличие тесной связи между успешностью сдачи ЕГЭ и принадлежностью учащегося к той или иной группе обучаемых.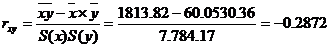
 непараметрические методы.
непараметрические методы. К. Спирмэном и
К. Спирмэном и  (8.9)
(8.9)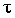 ) можно определить по формуле
) можно определить по формуле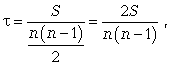 (8.10)
(8.10) ; n - общая сумма частот.
; n - общая сумма частот. (8.11)
(8.11) (8.12)
(8.12) (8.13)
(8.13) - показатель средней квадратической сопряженности:
- показатель средней квадратической сопряженности:
 (8.14)
(8.14) Кф
Кф 







 *
*



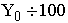



 и
и  . И если они различаются существенно (более 10%), то признается наличие тренда.
. И если они различаются существенно (более 10%), то признается наличие тренда.
 – среднее число серий в ряду, определяемое по формуле:
– среднее число серий в ряду, определяемое по формуле:  ;
;  – среднее квадратическое отклонение числа серий в ряду, определяемое по формуле
– среднее квадратическое отклонение числа серий в ряду, определяемое по формуле  .
. .
.


