
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретические кривые распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Допустим, что распределение непрерывного признака изображается графически гистограммой с равными интервалами и по оси ординат отложены плотности распределения. Если число наблюдений неограниченно растет, а длина интервала стремится к нулю, то ступенчатая гистограмма превращается в плавную кривую, называемую кривой распределения. При изучении закономерностей распределения значений признака в вариационном ряду выдвигают гипотезу о виде теоретической кривой распределения. Анализируя частоты в эмпирическом распределении, можно проверить правильность выдвинутой гипотезы. Знание вида теоретической кривой распределения упрощает его анализ и вычисление показателей распределения. Нормальное распределение Чаще всего наблюдаемые значения признака являются случайной величиной. Случайной величиной называется величина, которая в результате опыта принимает одно и только одно возможное значение, заранее не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Распределение непрерывной случайной величины x называется нормальным, если соответствующая ему кривая распределения описывается выражением
где x – значение признака;
Нормальное распределение наиболее часто встречается в практике. Кривая нормального распределения имеет следующий вид (рис. 6)
Рис. 6. Кривая нормального распределения Вид распределения определяется двумя параметрами
Рис. 7. Кривые нормального распределения при различных . При увеличении дисперсии


 
Рис. 8. Кривые нормального распределения при различных s 2 Свойства кривой нормального распределения. 1. Кривая симметрична и имеет максимум в точке 2. Значения 3. Кривая асимптотически приближается к оси абсцисс при x ® ±¥. Это означает, что чем больше значение x отклоняется от 4. Кривая имеет две точки перегиба на расстоянии ± s от 5. Правило 3 s: в промежутке [
          


 
Рис. 9. Правило 3 s Построение теоретической кривой распределения по эмпирическим данным называется выравниванием вариационного ряда. Порядок расчета теоретических частот кривой нормального распределения по эмпирическим данным. 1. По эмпирическим данным рассчитать среднее значение вариационного ряда 2. Вычислить нормированное отклонение каждого варианта от среднего значения
3. По таблице распределения функции
вычислить ее значения для всех t. 4. Вычислить теоретические частоты m' по формуле
где N – численность совокупности; hk – длина k- го интервала. В случае равных интервалов Распределение Пуассона Распределение Пуассона наблюдается в совокупностях, число единиц которых достаточно велико (N ≫100), а доля единиц, обладающих большими значениями признака мала. Распределение Пуассона описывает число заявок, поступающих в единицу времени в систему массового обслуживания. Распределение Пуассона описывается формулой (рис.10)
где P (x) – вероятность того, что признак примет значение x.
Рис. 10. Распределение Пуассона
Порядок расчета теоретических частот кривой распределения Пуассона по эмпирическим данным. 1. Найти среднее арифметическое значение вариационного ряда 2. Вычислить значение e-a. 3. Для каждого значения x вычислить теоретическую частоту по формуле
где N – число единиц в совокупности.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.13.194 (0.008 с.) |

 ,
, – среднее арифметическое значение признака;
– среднее арифметическое значение признака; – дисперсия значений признака.
– дисперсия значений признака.

 . При увеличении
. При увеличении 


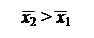




 +3 s
+3 s


 ,
, .
. ,
, – среднее арифметическое значение признака.
– среднее арифметическое значение признака.
 .
. .
.


