
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плотность распределения вероятностей СВСодержание книги
Поиск на нашем сайте
Плотностью распределения СВ (дифференциальной функцией распределения) называется такая функция р (х), что Свойства плотности распределения: 1) 2) 3) 4) Чтобы задать закон распределения непрерывной СВ необходимо задать или плотность распределения, или функцию распределения. Пример 5.1. Партия изделий содержит 10 % нестандартных. Пусть СВ Х – число стандартных изделий в партии из пяти изделий. Требуется составить закон распределения СВ и записать функцию распределения. Решение. СВ Х может принимать значения хk = 0, 1, 2, 3, 4, 5. Вероятность
Запишем закон распределения СВ
Найдем функцию распределения. По определению:
При при при при при при при Окончательно
Пример 5.2. Непрерывная СВ задана плотностью распределения:
Требуется найти значение параметра с и записать функцию распределения. Решение. Значение параметра с определим, используя свойство плотности распределения:
Функцию распределения определим из условия Для для для Значит,
Пример 5.3. Дана функция распределения СВ:
Нужно определить плотность распределения. Решение. Плотность распределения определим из свойства плотности распределения:
Числовые характеристики СВ К числовым характеристикам СВ относятся: математическое ожидание М (Х), дисперсия D (Х), среднее квадратическое отклонение s(Х), начальные и центральные моменты и др.
Математическое ожидание и его свойства Дискретная СВ принимает значения
Если непрерывная СВ задана плотностью распределения Математическое ожидание характеризует среднее значениеСВ. Свойства математического ожидания: 1) 2) 3) 4)
Дисперсия и ее свойства Начальным моментом k-го порядка называется математическое ожидание СВ Хk. Для дискретных случайных величин
Для непрерывных случайных величин
Центральным моментом k-ого порядка называется математическое ожидание СВ Для дискретных случайных величин:
Для непрерывных случайных величин:
Дисперсией называется центральный момент второго порядка:
Дисперсия характеризует степень разброса значений СВ относительно математического ожидания. Дисперсия СВ равна разности математического ожидания квадрата СВ и квадрата математического ожидания.
Свойства дисперсии: 1) 2) 3) 4) Средним квадратическим отклонением СВ называется корень квадратный из дисперсии СВ:
Пример 6.1. Дискретная СВ задана законом распределения. Требуется найти М (Х), D (X), s(X).
Решение.
Пример 6.2. Непрерывная СВ задана плотностью распределения:
Требуется вычислить М (Х), D (X), s(X). Решение.
Законы распределения СВ Законы распределения дискретных СВ СВ Х, которая принимает значения 0, 1, 2,¼, n с вероятностями
Для биномиального закона Дискретная СВ Х называется распределенной по закону Пуассона, если она принимает целые неотрицательные значения 0, 1, 2,¼, n … с вероятностями, которые определяются по формуле Пуассона:
Для закона Пуассона Пример 7.1. Производится 3 независимых испытания, в каждом из которых событие A появляется с вероятностью 0,4. СВ Х – число появлений события А. Требуется составить закон распределения и вычислить числовые характеристики. Решение. СВ Х принимает значения 0, 1, 2, 3, 4 и распределена по биномиальному закону. Определим вероятности:
Закон распределения имеет вид:
Пример 7.2. Телефонная станция обслуживает 400 абонентов. Вероятность того, что в течение часа абонент позвонит на станцию, равна 0,01 и постоянна для всех абонентов. Найти вероятность того, что на станцию в течение часа позвонят не более двух абонентов. Решение. По условию задачи п = 400, р = 0,01, т £ 2, l = 4.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.121.24 (0.009 с.) |

 .
. ;
; ;
; ;
; .
. найдем по формуле Бернулли:
найдем по формуле Бернулли:  . По условию задачи
. По условию задачи 

 .
. ,
, ,
, ,
, ,
, ,
, .
. .
. ,
, ,
, ,
, ,
, ,
, ,
,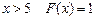 .
.

 .
. .
. .
. ,
, ,
, .
.

 .
.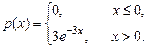
 с вероятностями
с вероятностями  . Математическим ожиданием СВ называется число М (Х), которое определяется соотношением
. Математическим ожиданием СВ называется число М (Х), которое определяется соотношением .
. , то математическое ожидание определяется интегралом
, то математическое ожидание определяется интегралом  .
. ;
; ;
; ;
; , если СВ X и Y независимы.
, если СВ X и Y независимы. .
. .
. .
. .
. .
. .
. .
. ;
; ;
; ;
; , X, Y – независимые СВ.
, X, Y – независимые СВ. .
. ,
, ,
, ,
, .
.
 ,
, ,
, ,
, .
. , называется распределенной по биномиальному закону. Биномиальный закон распределения может быть представлен в виде таблицы:
, называется распределенной по биномиальному закону. Биномиальный закон распределения может быть представлен в виде таблицы:

 .
. .
. .
. ,
, ,
, ,
, ,
, .
.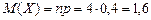 ,
, ,
, .
.



