
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборки. Эмпирическая функция распределенияСодержание книги
Поиск на нашем сайте
Изучение всего набора элементов генеральной совокупности часто оказывается невозможным из-за больших материальных затрат или бесконечности генеральной совокупности. В этом случае применяется выборочный метод. Сущность выборочного метода заключается в том, что из генеральной совокупности извлекается выборка. На выборке производят нужные исследования, а полученные результаты распространяют на всю совокупность. Пусть для изучения количественного признака Х из генеральной совокупности извлечена выборка Статистическое распределение выборочной совокупности можно представить графически в виде полигона или гистограммы. Полигоном частот выборочной совокупности называется ломаная линия, соединяющая точки с координатами Гистограммой выборочной совокупности называется фигура, составленная в декартовой системе координат из прямоугольников, основаниями которых являются частичные интервалы Эмпирической функцией распределения называется функция 1) 2) эмпирическая функция распределения является неубывающей функцией, т. е. если 3) если
Точечные оценки неизвестных параметров распределения Статистической оценкой неизвестного параметра генеральной совокупности называется функция от наблюдаемых значений случайной величины Х. Сами наблюдаемые значения (варианты) Статистическая оценка называется точечной, если она определяется одной величиной. Точечная оценка, математическое ожидание которой равно оцениваемому параметру, называется несмещенной, в противном случае – смещенной. Несмещенной оценкой для математического ожидания генеральной совокупности является
Смещенной оценкой для дисперсии генеральной совокупности является выборочная дисперсия
Оценка Один и тот же параметр может иметь несколько оценок, которые обладают различными дисперсиями при ограниченном числе опытов. Чем меньше эта дисперсия, тем меньше вероятность совершить ошибку при оценке параметра. Поэтому в качестве оценки берется та, которая обладает минимальной дисперсией (эффективная).
Интервальные оценки неизвестных параметров Распределения Статистическая оценка называется интервальной, если она характеризуется двумя случайными величинами: началом и концом интервала. В качестве интервальной оценки используются доверительные интервалы. Пусть Доверительный интервал для неизвестного математического ожидания нормально распределенной СВ при известном среднем квадратическом отклонении s генеральной совокупности определяется неравенством
где t – значение функции Лапласа Если среднее квадратическое отклонение σ нормально распределенной СВ неизвестно, но по результатам выборки вычислены
где Доверительный интервал для среднего квадратического отклонения s нормально распределенной СВ определяется неравенством
где
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 211; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.98.91 (0.008 с.) |

 объема n. Наблюдаемые значения хi признака Х называют вариантами, а последовательность вариантов, записанную в возрастающем порядке, – вариационным рядом. Статистическим распределением выборки называется перечень хi и соответствующих им частот тi или относительных частот v i.
объема n. Наблюдаемые значения хi признака Х называют вариантами, а последовательность вариантов, записанную в возрастающем порядке, – вариационным рядом. Статистическим распределением выборки называется перечень хi и соответствующих им частот тi или относительных частот v i. .
. , а высоты соответственно равны
, а высоты соответственно равны  , где
, где  .
. , где nх – число вариант в выборке, меньших х; п – объем выборки. Эмпирическая функция распределения при больших п служит оценкой неизвестной функции распределения генеральной совокупности. Эмпирическая функция распределения обладает следующими свойствами:
, где nх – число вариант в выборке, меньших х; п – объем выборки. Эмпирическая функция распределения при больших п служит оценкой неизвестной функции распределения генеральной совокупности. Эмпирическая функция распределения обладает следующими свойствами: ;
; , то
, то  ;
; – наименьшая варианта, а
– наименьшая варианта, а  – наибольшая варианта, то
– наибольшая варианта, то  при
при  и
и  при
при  .
. рассматриваются как значения п независимых СВ
рассматриваются как значения п независимых СВ 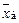 – выборочная средняя:
– выборочная средняя: .
. , а несмещенной оценкой для дисперсии генеральной совокупности является исправленная выборочная дисперсия
, а несмещенной оценкой для дисперсии генеральной совокупности является исправленная выборочная дисперсия  .
. ,
, ,
,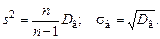
 параметра q называется состоятельной, если она сходится по вероятности к оцениваемому параметру при неограниченном числе испытаний, т. е. для любого сколь угодно малого e > 0 выполнено предельное равенство
параметра q называется состоятельной, если она сходится по вероятности к оцениваемому параметру при неограниченном числе испытаний, т. е. для любого сколь угодно малого e > 0 выполнено предельное равенство  .
. является статистической оценкой неизвестного параметра q. Тогда при некоторых e > 0 вероятность
является статистической оценкой неизвестного параметра q. Тогда при некоторых e > 0 вероятность  близка к единице, т. е. неизвестный параметр q с вероятностью g накрывается интервалом
близка к единице, т. е. неизвестный параметр q с вероятностью g накрывается интервалом  . Вероятность g называется доверительной вероятностью или надежностью оценки. Интервал, который с заданной надежностью накрывает неизвестный параметр, называется доверительным интервалом.
. Вероятность g называется доверительной вероятностью или надежностью оценки. Интервал, который с заданной надежностью накрывает неизвестный параметр, называется доверительным интервалом. ,
, , при котором
, при котором 
 и s, то доверительный интервал для математического ожидания определяется неравенством
и s, то доверительный интервал для математического ожидания определяется неравенством
 находится из таблицы (приложение 5) по заданным значениям g и n.
находится из таблицы (приложение 5) по заданным значениям g и n.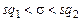 ,
,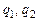 определяются из таблицы (приложение 6) по заданным g и ν = n – 1.
определяются из таблицы (приложение 6) по заданным g и ν = n – 1.


