
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая проверка гипотезы о нормальномСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Распределении Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Важнейшим среди законов распределения является нормальный закон распределения с функцией распределения
Нормальный закон распределения является предельным для ряда законов распределения. Поэтому основные методы математической статистики разработаны применительно для нормального закона. Пусть Одним из методов статистической проверки гипотезы о законе распределения является критерий согласия Пирсона
По результатам выборки вычисляем выборочное среднее
Определим теоретические вероятности попадания СВ в интервал (
Вычисляем теоретические частоты
Из таблицы критических точек распределения Пирсона Если Пример 8.1. Дано статистическое распределение срока службы инструмента до выхода за пределы точности (в месяцах).
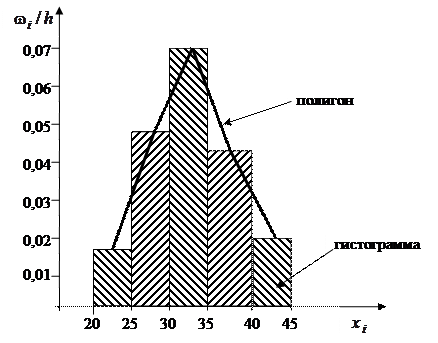
Требуется: 1) построить полигон и гистограмму относительных частот (частостей); 2) по виду полигона и гистограммы и, исходя из механизма образования исследуемой СВ, сделать предварительный выбор закона распределения; 3) предполагая, что СВ распределена по нормальному закону, найти точечные оценки параметров распределения, записать гипотетичную функцию распределения; 4) найти теоретические частоты нормального распределения и проверить гипотезу о нормальном распределении с помощью критерия Пирсона 5) найти доверительные интервалы для математического ожидания и среднего квадратического отклонения нормально распределенной СВ при надежности Решение. Вычислим относительные частоты
Построим гистограмму и полигон частостей.
Так как полигон частостей приближенно представляет кривую Гаусса и срок службы инструмента зависит от большого количества независимых параметров, то можно сделать предположение о нормальном распределении срока службы инструмента. Вычислим точечные оценки параметров распределения.
Запишем гипотетичную функцию распределения
Вычислим теоретические частоты в предположении, что СВ распределена по нормальному закону:
Вычисления значений функции Лапласа приведены в таблице.
Вычислим теоретические частоты.
Проверим гипотезу о нормальном распределении с помощью критерия Вычислим статистику Пирсона.
Из таблицы критических точек распределения Найдем доверительные интервалы для а и s.
КОНТРОЛЬНЫЕ ЗАДАНИЯ 1. Установлены три независимо работающих пожарных извещателя. Вероятности того, что при пожаре сработает первый, второй и третий извещатель соответственно равны 0,9, 0,7, 0,85. Какова вероятность того, что при пожаре сработает хотя бы одно устройство? 2. Для подготовки к экзамену студент должен изучить 50 теоретических вопросов и научиться решать 30 типов задач. Студент, готовясь к экзамену, выучил 40 теоретических вопросов и научился решать 25 типов задач. Найти вероятность того, что студент сдаст экзамен, если для сдачи экзамена достаточно ответить на любые два задания из билета, содержащего два теоретических вопроса и задачу. 3. Детали проходят четыре операции обработки. Вероятность получения брака при первой, второй, третьей и четвертой операциях соответственно равны 0,005, 0,01, 0,015, 0,02. Найти вероятность того, что после четырех операций будет получена стандартная деталь. 4. У сборщика 10 деталей, из них первого сорта 6, второго – 4. Какова вероятность того, что из 5 одновременно взятых деталей 3 окажутся первого сорта и 2 – второго сорта? 5. Прибор состоит из трех независимо работающих блоков. Вероятности выхода из строя за время Т первого, второго, третьего блоков соответственно равны 0,1, 0,05, 0,01. Каждый блок необходим для работы прибора в целом. Какова вероятность того, что за время Т прибор выйдет из строя? 6. В ящике 15 деталей, среди которых 12 окрашенных. Сборщик наугад извлекает 5 деталей. Какова вероятность того, что среди извлеченных деталей 3 будут окрашенными? 7. В мастерской работают два мотора независимо друг от друга. Вероятность того, что в течение смены первый мотор не потребует внимания мастера равна 0,85, а для второго мотора эта вероятность равна 0,7. Найти вероятность того, что в течение смены только один мотор потребует внимания мастера. 8. Найти вероятность того, что случайно взятое изделие окажется первосортным, если известно, что 4 % всей продукции является браком, а 80 % небракованной продукции удовлетворяют требованиям первого сорта. 9. Устройство содержит три независимо работающих блока. Вероятности отказов блоков соответственно равны 0,15, 0,2, 0,1. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один из блоков. 10. Три исследователя независимо один от другого производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора равна 0,01. Для второго и третьего исследователей эти вероятности равны 0,02 и 0,015. Найти вероятность того, что ошибка будет допущена при измерении не более, чем одним исследователем. 11. В контейнере 17 изделий, из них 10 изделий первого сорта, 4 изделия – 2-ого сорта и 3 изделия – 3-ого сорта. Рабочий случайным образом берет 6 изделий. Какова вероятность того, что среди взятых изделий первого сорта окажется 3 изделия, второго – 2 изделия, третьего – 1 изделие? 12. В течение года три фирмы могут обанкротиться независимо друг от друга соответственно с вероятностями 0,02, 0,05, 0,04. Какова вероятность того, что в конце года все фирмы будут функционировать? 13. На сессии студенту предстоит сдать экзамены по четырем предметам. Студент освоил 90 % вопросов по первому предмету, 80 % – по второму, 75 % – по третьему и 95 % – по четвертому. Какова вероятность того, что студент успешно сдаст сессию? 14. Устройство состоит из четырех элементов, из которых два изношены. При включении устройства включаются случайным образом два элемента. Какова вероятность того, что включенными будут неизношенные элементы? 15. В электрическую цепь включено последовательно три элемента, работающие независимо друг от друга. Вероятности отказа элементов соответственно равны 0,2, 0,15, 0,1. Найти вероятность того, что тока в цепи не будет. 16. Из партии для контроля отбирают 3 изделия. Известно, что в партии содержится 20 изделий, из которых 4 бракованных. Найти вероятность того, что среди отобранных все изделия годные. 17. На фирме 550 работников, 380 из них имеют высшее образование, а 412 – среднее специальное образование, у 357 работников – высшее и среднее специальное образование. Чему равна вероятность того, что случайно выбранный работник имеет высшее или среднее образование или то и другое? 18. В ремонтную мастерскую поступило 8 телевизоров, из них 5 нуждается в общей регулировке. Мастер случайным образом берет для ремонта четыре телевизора. Какова вероятность того, что из выбранных телевизоров 3 нуждаются в общей регулировке? 19. Из группы туристов, отправляющихся за границу, 60 % владеют английским языком, 40 % – французским и 10 % – обоими языками. Найти вероятность того, что наугад взятый турист будет нуждаться в переводчике. 20. В читальном зале 10 учебников по теории вероятности, из которых 4 в твердом переплете. Библиотекарь берет один за другим два учебника. Найти вероятность того, что оба учебника окажутся в мягком переплете. 21. Вероятность того, что студент выполнит без ошибок лабораторную работу по физике, равна 0,7, а по химии – 0,8. Какова вероятность того, что он выполнит без ошибок: а) обе лабораторные работы; б) только одну из них; в) хотя бы одну лабораторную работу? 22. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наугад взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных изделий только два изделия высшего сорта. 23. Устройство состоит из трех элементов, работающих независимо. Вероятности безотказной работы (за время t) первого, второго и третьего элементов соответственно равны 0,6, 0,7, 0,8. Найти вероятности того, что за время t безотказно будут работать: а) только один элемент; б) только два элемента; в) все три элемента. 24. В ящике 10 деталей, из которых 4 окрашены. Сборщик наугад взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена. 25. Для студента второго курса вероятность решить правильно задачу № 1 из типового расчета равна 0,8, а задачу № 2 – 0,7. Какова вероятность того, что: а) студент правильно решит обе задачи; б) решит неправильно хотя бы одну из задач; в) решит верно только одну из задач? 26. Две фотомодели снимаются для журнала мод. Вероятность появления в журнале их фотографий соответственно равна 0,9 и 0,7. Какова вероятность того, что в следующем номере журнала появятся снимки: а) обеих девушек; б) только первой; в) хотя бы одной из них? 27. Вероятность того, что наугад выбранный компьютер работает со сбоем, равна 0,2. Оператор включил два компьютера. Какова вероятность того, что: а) хотя бы один из них будет работать без сбоев; б) оба компьютера будут исправны. 28. Два скрипача участвуют в конкурсе. Вероятность стать лауреатом конкурса для первого музыканта равна 0,7, для второго – 0,6. Какова вероятность того, что: а) хотя бы один из них станет лауреатом; б) лауреатами станут оба скрипача? 29. Автомеханик находит неисправность генератора автомобиля с вероятностью 0,8, карбюратора – 0,9. Какова вероятность того, что при очередной поломке автомобиля: а) он обнаружит хотя бы одну из поломок; б) не обнаружит неисправностей генератора и карбюратора? 30. Два баскетболиста делают по одному броску мячом по корзине. Для первого спортсмена вероятность попадания равна 0,7, для второго – 0,9. Какова вероятность того, что в корзину попадут: а) оба игрока; б) хотя бы один из них; в) попадет только первый спортсмен? 31. В ящике содержится 12 деталей, изготовленных на заводе № 1, 20 деталей – на заводе № 2 и 18 деталей – на заводе № 3. Вероятность того, что деталь, изготовленная на заводе № 1, отличного качества, равна 0,9; для деталей, изготовленных на заводах № 2 и № 3, эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наугад деталь окажется отличного качества. 32. Соотношение грузовых автомобилей, проезжающих по шоссе, на котором стоит бензоколонка, к числу легковых машин, проезжающих по тому же шоссе, равно 3: 2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина. 33. В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки. 34. В специализированную больницу поступают в среднем 50 % больных с заболеванием К, 30 % – с заболеванием L, 20 % – с заболеванием M. Вероятность полного излечения болезни К равна 0,7; для болезней L и M. эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием К. 35. В продажу поступают телевизоры трех заводов. Продукция первого завода содержит 20 % телевизоров со скрытым дефектом, второго – 10 % и третьего – 5 %. Какова вероятность приобрести исправный телевизор, если в магазин поступило 30 % телевизоров с первого завода, 20 % – со второго и 50 % – с третьего? 36. У стоматолога три вида пломбирующего материала: цемент (50 %), амальгама (30 %) и пластмасса (20 %). Условия лечения таковы, что вероятность выпадения пломбы, сделанной из цемента, в течение первого года после лечения равна 0,5, пломбы из амальгамы – 0,6, из пластмассы – 0,4. У пациента пломба выпала через неделю. Из какого материала вероятнее всего она была сделана, если врач взял тот пломбирующий материал, что оказался под рукой? 37. Прибор, установленный на борту самолета, может работать в двух режимах: в условиях нормального крейсерского полета и в условиях перегрузки при взлете и посадке. Крейсерский режим осуществляется в 80 % всего времени полета, режим перегрузки – в 20 %. Вероятность выхода прибора из строя за время полета в нормальном режиме равна 0,1, в условиях перегрузки – 0,4. Найти вероятность отказа прибора за время полета. 38. Для участия в математической олимпиаде среди студентов университета из группы № 1 выбрано 4 студента, из группы № 2 – 6 и из группы № 3 – 5. Вероятность того, что студент попадет в команду факультета, для этих групп соответственно равна 0,9, 0,8 и 0,5. Наугад выбранный студент в итоге попал в команду. В какой из групп вероятнее всего он учится? 39. На склад поступают диваны с трех мебельных фабрик. Первая и третья фабрики изготавливают одинаковое количество продукции, а вторая – вдвое больше. Вероятность для первой, второй и третьей фабрики сделать бракованный диван равна 0,15, 0,05 и 0,1 соответственно. Какова вероятность того, что диван, купленный наудачу, качественный? 40. Экзаменационные работы по математике с вероятностью 0,2, 0,3 и 0,5 попадают на проверку к одному из трех экзаменаторов, каждый из которых может пропустить (не заметить) ошибку студента с вероятностью 0,01, 0,02 и 0,015 соответственно. Наугад выбранная работа (из числа проверенных) оказалась правильно аттестованной. Какова вероятность, что эту работу проверял третий преподаватель? 41. С первого станка на сборку поступает 30 %, со второго – 40 %, с третьего – 30 % общего количества деталей. Среди деталей, изготовленных на первом станке, имеется 2 % брака, на втором – 3 %, на третьем – 1 % брака. Найти вероятность того, что поступившая на сборку деталь стандартная. 42. Изделие проверяется на стандартность одним из двух контролеров. Первый контролер проверяет 55 % общего количества изделий, второй – 45 %. Вероятность того, что стандартное изделие будет признано стандартным первым контролером, равна 0,9; а вторым – 0,85. Стандартное изделие при проверке признано стандартным. Найти вероятность того, что изделие проверял второй контролер. 43. Партия электролампочек на 25 % изготовлена первым заводом, на 35 % – вторым, на 40 % – третьим. Вероятности выпуска брака первым, вторым и третьим заводом соответственно равны 0,01, 0,02, 0,05. Найти вероятность того, что случайно взятая лампочка окажется бракованной. 44. На складе находятся детали, изготовленные на двух заводах. Объем продукции первого завода в четыре раза больше объема продукции второго. Вероятность брака на первом заводе 0,05; на втором – 0,01. Наудачу взятая деталь оказалась бракованной. Какова вероятность того, что деталь изготовлена первым заводом? 45. Курс доллара повышается в течение квартала с вероятностью 0,9 и понижается с вероятностью 0,1. При повышении курса доллара фирма рассчитывает получить прибыль с вероятностью 0,85; при понижении – с вероятностью 0,3. Найти вероятность того, что фирма получит прибыль. 46. В цехе работает 15 станков. Из них 10 станков марки А, 3 – марки В и 2 – марки С. Вероятности выпуска стандартной детали на этих станках соответственно равны 0,85, 0,8, 0,9. При проверке деталь оказалась бракованной. Какова вероятность того, что она выпущена на станке марки С. 47. Среди студентов факультета – 35 % составляют первокурсники, 30 % студентов учатся на втором курсе, на 3-м и 4-м курсах их соответственно 20 % и 15 %. Среди студентов первого курса сдали сессию на отлично 3 %, среди второкурсников – 4,5 %, среди третьекурсников – 7 %, а среди студентов 4 курса – 10 %. Наугад вызванный студент оказался отличником. Какова вероятность того, что он учится на третьем курсе? 48. На сборку поступают детали с 2-х автоматов. Первый автомат дает в среднем 2 % брака, второй – 1 %. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 5000 деталей, со второго – 3000 деталей. 49. В двух ящиках имеются однотипные детали. В первом ящике 20 деталей, из них две бракованные, во втором – 30, из них 5 бракованных. Наугад взятая деталь из случайно выбранного ящика оказалась бракованной. Найти вероятность того, что она взята из первого ящика. 50. Аппаратура в 80 % случаях работает в нормальном режиме и в 20 % – в аварийном. Вероятность сбоя в нормальном режиме равна 0,05; в аварийном – 0,5. Найти вероятность сбоя аппаратуры. 51. На наблюдательной станции установлены три радиолокатора различных конструкций. Вероятность обнаружения цели первым локатором равна 0,86; вторым – 0,7; третьим – 0,9. Оператор случайным образом включает один из локаторов и обнаруживает цель. Какова вероятность того, что был включен второй локатор? 52. Вероятность, что выпущенная деталь окажется годной, равна 0,96. Деталь подвергается упрощенной схеме контроля, которая для годных деталей дает положительный результат с вероятностью 0,95, а для деталей с отклонениями – с вероятностью 0,08. Какова вероятность того, что изделие, прошедшее упрощенный контроль, является годным? 53. Производится три независимых выстрела по самолету. Вероятность попадания в самолет при каждом выстреле равна 0,3. Самолет сбивается при одном попадании с вероятностью 0,2; при двух попаданиях – 0,5; при трех – 0,9. В результате трех выстрелов самолет сбит. Какова вероятность того, что было два попадания? 54. Радиолампа может принадлежать к одной из трех партий с вероятностями: 0,25, 0,25, 0,5. Вероятности того, что радиолампа проработает гарантийный срок для первой, второй и третьей партий соответственно равны 0,9, 0,8, 0,85. Найти вероятность того, что наугад взятая электролампа выдержит гарантийный срок. 55. В торговую сеть поступают однотипные изделия, выпущенные тремя фабриками. Первая фабрика выпускает 30 % общего количества изделий, вторая – 50 %, третья – 20 %. Продукция первой фабрики содержит 0,5 % брака, второй – 2 %, третьей – 1 %. Какова вероятность того, что купленное изделие не будет бракованным? 56. Деталь производится одним из трех автоматов. Производительность первого автомата в два раза больше производительности второго автомата, а производительность третьего автомата в полтора раза больше производительности второго автомата. Брак первого, второго и третьего автоматов составляет соответственно 1 %, 2 %. 4 %. Какова вероятность выпуска стандартной детали? 57. Прибор может собираться из высококачественных деталей и из деталей обычного качества. Из высококачественных деталей собирается 40 % общего количества приборов. Вероятности выхода из строя прибора в течение гарантийного срока, собранного из высококачественных деталей, равна 0,03; собранного из деталей обычного качества – 0,1. Прибор выдержал гарантийный срок. Какова вероятность того, что прибор собирался из обычных деталей? 58. На трех автоматических линиях изготавливаются однотипные детали. Вследствие разладки станков возможен выпуск бракованной продукции первой линией с вероятностью 0,01; второй – 0,015; третьей – 0,02. Первая линия выпускает 30 % общего количества деталей, вторая –20 %, третья – 50 %. Найти вероятность выпуска брака. 59. Партия микросхем содержит 10 % брака. Проверка микросхем такова, что с вероятностью 0,98 обнаруживается дефект (если он есть) и с вероятностью 0,03 стандартная микросхема признается бракованной. Какова вероятность того, что на самом деле микросхема стандартна? 60. Две из трех независимо работающих ламп отказали. Найти вероятность того, что отказали первая и третья лампы, если вероятности отказа первой, второй и третьей ламп соответственно равны 0,1, 0,3, 0,4. 61. В телевизионной студии 4 камеры. Для каждой камеры вероятность того, что она включена в данный момент, равна 0,8. Найти вероятность того, что в данный момент включено не менее двух камер. 62. Рабочий обслуживает 8 однотипных станков. Вероятность того, что в течение времени T станок потребует внимания рабочего, равна 0,6. Найти вероятность того, что в течение времени T не менее 7 станков потребуют внимания рабочего. 63. В течение гарантийного срока выходит из строя в среднем 5 % телевизоров. Какова вероятность того, что в партии из 100 телевизоров выдержат гарантийный срок не менее 60 телевизоров? 64. Вероятность выздоровления больного в результате применения нового способа лечения равна 0,98. Какова вероятность того, что из 100 больных, подвергшихся новому лечению, выздоровевших будет не менее 95? 65. Завод отправил на базу 5000 лампочек. Вероятность повреждения лампочки при перевозке равна 0,0002. Найти вероятность того, что при перевозке поврежденными окажутся 3 лампочки. 66. Вероятность того, что прибор не выдержит испытание, равна 0,001. Найти вероятность того, что из 1000 приборов более одного не выдержат испытание. 67. При передаче сообщения вероятность искажения одного знака равна 0,2. Какова вероятность того, что сообщение из 6 символов содержит не более одного искаженного символа? 68. Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение часа равна 0,0005. Какова вероятность того, что в течение часа нить оборвется на 3 веретенах? 69. В комнате 5 электрических лампочек, каждая из которых перегорает в течение года с вероятностью 0,7. Найти вероятность того, что в течение года перегорит не менее двух электролампочек. 70. Вероятность сбоя в АТС при каждом вызове равна 0,0002. Определить вероятность того, что при 5000 вызовов произойдет не более двух сбоев. 71. По данным отдела технического контроля на 100 металлических брусков, заготовленных для обработки, приходится 30 с зазубринами. Какова вероятность того, что из семи случайно взятых брусков не более двух окажутся с дефектом? 72. Телефонная станция обслуживает 600 абонентов. Вероятность звонка абонента в течение часа равна 0,005. Какова вероятность того, что в течение часа поступят звонки не более чем от трех абонентов? 73. В 30 % случаев страховая компания выплачивает по договору страховку. Найти вероятность того, что по истечении срока 10 договоров компания уплатит страховку в трех случаях. 74. Прибор состоит из пяти узлов. Вероятность безотказной работы в течение смены каждого узла равна 0,8. Причем работа каждого узла необходима для работы прибора в целом. Найти вероятность того, что в течение смены прибор выйдет из строя. 75. Вероятность реализации одной акции некоторой компании равна 0,8. Брокерская контора предлагает 100 акций этой компании. Какова вероятность того, что будет продано не менее 85 акций? 76. Завод отправил потребителю партию из 500 изделий. Вероятность повреждения изделия в пути равна 0,003. Найти вероятность того, что в пути будет повреждено не более двух изделий. 77. Вероятность отказа прибора при испытании равна 0,15. Какова вероятность того, что из 10 приборов при испытании откажут не более 2 из них? 78. Агрегат состоит из 21 блока. Вероятность того, что за время Т произвольный блок испытывает лишь допустимые деформации, равна 0,8. Найти вероятность того, что за время Т испытывают такие деформации от 18 до 20 блоков. 79. На склад поступают изделия, из которых 80 % оказываются высшего сорта. Найти вероятность того, что из 100 наудачу взятых изделий, не менее 80 окажутся высшего сорта. 80. При установившемся технологическом процессе 70 % всего числа изделий выпускается высшего сорта. Отдел технического контроля испытывает 200 изделий. Найти вероятность того, что изделий высшего сорта окажется в пределах от 140 до 180. 81. Инженерное сооружение состоит из семи узлов, вероятность разрушения каждого из которых 0,2. Сооружение считается разрушенным, если разрушено не менее трех узлов. Какова вероятность разрушения сооружения? 82. Книга из 500 страниц имеет 40 опечаток. Какова вероятность того, что на случайно выбранной странице не более одной опечатки? 83. В магазин вошло десять покупателей. Найти вероятность того, что 4 из них совершат покупки, если вероятность совершить покупку для каждого покупателя равна 0,3. 84. Среди 100 изготавливаемых микросхем в среднем одна бракованная. Найти вероятность того, что в партии из 1000 микросхем будет не более двух бракованных. 85. В цехе 80 станков одинаковой мощности, работающих независимо друг от друга в одинаковом режиме, при котором их привод оказывается включенным в течение 0,8 всего рабочего времени. Какова вероятность того, что в произвольно взятый момент времени окажутся включенными от 60 до 70 станков? 86. При массовом производстве шестерен вероятность брака 0,001. Какова вероятность того, что из 500 шестерен не более трех окажутся бракованными? 87. В ходе аудиторской проверки компании аудитор случайным образом отбирает пять счетов. Найти вероятность того, что он обнаружит не более одного счета с ошибкой, если ошибки содержат в среднем 3 % счетов. 88. Сборник содержит 400 задач с ответами. В каждом ответе вероятность ошибки 0,01. Какова вероятность того, что в сборнике не более двух задач с ошибочными ответами? 89. Каждое из 8 предприятий отрасли выполняет месячный план с вероятностью 0,9. Найти вероятность того, что месячный план выполняет не менее шести предприятий. 90. При передаче текстовой информации слова кодируются в символы. Вероятность искажения каждого символа при передаче равна 0,009. При искажении двух и более символов слово не поддается дешифровке. Найти вероятность того, что слово, содержащее 10 символов, будет принято правильно. В задачах 91–120 требуется для данной СВ Х: 1) составить закон распределения СВ; 2) найти математическое ожидание М (Х) и дисперсию D (X); 3) найти функцию распределения F (x). 91. В партии из шести изделий имеются два бракованных. Наугад взято три изделия. СВ Х – количество стандартных изделий среди трех взятых изделий. 92. Имеются три заготовки для одной и той же детали. Вероятность изготовления стандартной детали из каждой заготовки равна 0,9. СВ Х – количество заготовок, оставшихся после изготовления первой стандартной детали. 93. Прибор состоит из трех узлов. Вероятности выхода узлов из строя в течение времени Т соответственно равны 0,1, 0,05, 0,2. СВ Х – число отказавших узловв течение времени Т. 94. Вероятность того, что в течение гарантийного срока телевизор потребует ремонта, равна 0,2. СВ Х – число телевизоров не выдержавших гарантийный срок из четырех приобретенных телевизоров. 95. Охотник, имеющий четыре патрона, стреляет в цель до первого попадания (или пока не израсходует все патроны). Вероятность попадания при каждом выстреле равна 0,7. СВ Х – число израсходованных патронов. 96. Стрелок делает три выстрела по мишени. Вероятности попадания в цель при первом, втором и третьем выстрелах соответственно равны 0,6, 0,7, 0,8. СВ Х – число попаданий в мишень. 97. В партии 10 % деталей нестандартных. Наугад взяты четыре детали. СВ Х – число нестандартных деталей из 4 взятых. 98. Сигнальное устройство состоит из трех независимо работающих элементов, вероятность отказа каждого из которых равна 0,2. СВ Х – число отказавших элементов. 99. В партии из 10 изделий содержится три бракованных. Наугад отобраны два изделия. СВ Х – число бракованных изделий среди отобранных. 100. Вероятность изготовления стандартного изделия при установившемся технологическом процессе постоянна и равна 0,9. Для проверки качества изделия берутся и проверяются одно за другим 4 изделия. Если обнаруживается бракованное изделие, то бракуют всю партию. СВ Х – число изделий, проверяемых ОТК из каждой партии. 101. Установлены три независимо работающих сигнализатора, которые срабатывают при пожаре с вероятностями 0,8, 0,7, 0,9. СВ X – количество сигнализаторов, сработавших при пожаре. 102. Баскетболист делает три броска в кольцо. Вероятности попадания в кольцо при первом, втором и третьем броске соответственно равны 0,5, 0,6, 0,7. СВ X – количество попаданий в кольцо. 103. Стрелок делает три выстрела в мишень. Вероятность попадания в мишень при каждом выстреле постоянна и равна 0,16. СВ X – число попаданий. 104. Три стрелка делают по одному выстрелу в мишень. Вероятности попадания в мишень для первого, второго и третьего стрелков соответственно равны 0,5; 0,6; 0,6. СВ X – количество попаданий в мишень. 105. Устройство состоит из трех блоков, которые выходят из строя за время Т с вероятностями 0,1, 0,05, 0,15. СВ X – количество блоков, вышедших из строя за время Т. 106. В партии из 6 изделий – 3 бракованных. Случайным образом взяты 3 изделия из партии. СВ X – количество бракованных изделий среди трех взятых. 107. Устройство состоит из трех блоков, которые выходят из строя за время Т с вероятностью 0,1. СВ X – количество блоков, которые вышли из строя за время Т. 108. В партии деталей – 5 % брака. Наугад из партии взято 3 детали. СВ X – количество бракованных деталей из взятых. 109. Монету подбрасывают 5 раз. СВ X – количество появлений герба. 110. В партии из 5 изделий одно бракованное. Чтобы его обнаружить, выбирают наугад одно изделие за другим и проверяют. СВ X – количество проверенных изделий. 111. Вероятность приема каждого из
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 610; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.014 с.) |

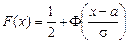 .
.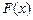 – функция распределения изучаемой СВ. Обозначим через Но гипотезу о нормальном распределении СВ с функцией
– функция распределения изучаемой СВ. Обозначим через Но гипотезу о нормальном распределении СВ с функцией 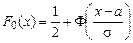 , где а и s – конкретные значения параметров распределения. Для проверки гипотезы проводят серию из n независимых испытаний. В результате получают выборочную совокупность
, где а и s – конкретные значения параметров распределения. Для проверки гипотезы проводят серию из n независимых испытаний. В результате получают выборочную совокупность  , по которой делают вывод о правильности гипотезы Но. Так как СВ может принимать бесчисленное множество значений, то выборочная совокупность содержит неполную информацию о законе распределения генеральной совокупности. По этой причине при проверке гипотезы Но может быть допущена ошибка. Вероятность ошибочного отклонения правильной гипотезы Но называется уровнем значимости. Обычно при проверке гипотезы уровень значимости a берут равным 0,001, 0,01, 0,05.
, по которой делают вывод о правильности гипотезы Но. Так как СВ может принимать бесчисленное множество значений, то выборочная совокупность содержит неполную информацию о законе распределения генеральной совокупности. По этой причине при проверке гипотезы Но может быть допущена ошибка. Вероятность ошибочного отклонения правильной гипотезы Но называется уровнем значимости. Обычно при проверке гипотезы уровень значимости a берут равным 0,001, 0,01, 0,05.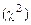 . Пусть статистическое распределение выборки задано в виде последовательности интервалов
. Пусть статистическое распределение выборки задано в виде последовательности интервалов 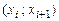 и соответствующих частот
и соответствующих частот 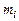 (
(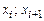
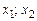
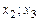
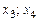
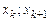
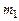
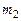
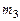
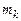
 и выборочное среднее квадратическое отклонение
и выборочное среднее квадратическое отклонение 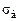 . Предположим (гипотеза Но), что СВ распределена нормально с параметрами
. Предположим (гипотеза Но), что СВ распределена нормально с параметрами 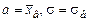 . Теоретическая функция распределения имеет вид
. Теоретическая функция распределения имеет вид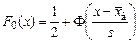 .
.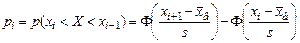 .
.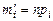 и вычисляем
и вычисляем 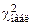 (статистику Пирсона):
(статистику Пирсона):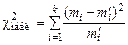 .
.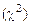 по заданному уровню значимости a и число степеней свободы ν = k – 3 (k – число интервалов) определяем критическое значение
по заданному уровню значимости a и число степеней свободы ν = k – 3 (k – число интервалов) определяем критическое значение 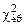 .
.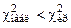 , то нет оснований отвергать гипотезу Н 0 о нормальном распределении генеральной совокупности. Если
, то нет оснований отвергать гипотезу Н 0 о нормальном распределении генеральной совокупности. Если 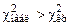 , то гипотеза Н 0 отвергается с вероятностью ошибки a.
, то гипотеза Н 0 отвергается с вероятностью ошибки a.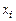 – срок службы в мес.
– срок службы в мес.
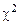 при уровне значимости
при уровне значимости 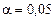 ;
;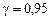 .
.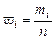 , середины интервалов
, середины интервалов 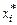 , высоты прямоугольников гистограммы
, высоты прямоугольников гистограммы 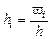 .
.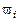
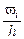
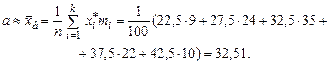
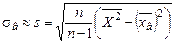 .
.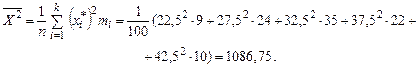
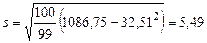 .
.
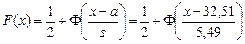 .
.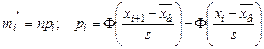 .
.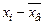
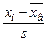
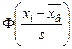
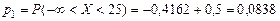 ,
,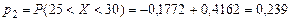 ,
,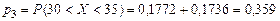 ,
,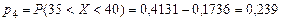 ,
,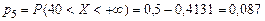 ,
,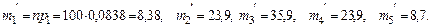
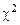 .
.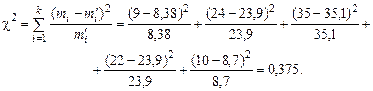
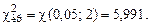 Так как
Так как 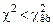 , то нет оснований отвергать гипотезу о нормальном распределении СВ.
, то нет оснований отвергать гипотезу о нормальном распределении СВ.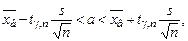
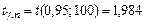 (приложение 5). Поэтому 31,433 < a < 33,587.
(приложение 5). Поэтому 31,433 < a < 33,587.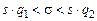 , где
, где 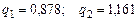 (приложение 6). Значит 4,82 < s < 6,37.
(приложение 6). Значит 4,82 < s < 6,37.


