
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 5. Проверка статистических гипотезСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Глава 5. Проверка статистических гипотез
В научных исследованиях для доказательства достоверности результатов эксперимента необходимо оценивать их значимость. Приходится сравнивать данные опыта с контрольными данными, причем о преимуществе одной из сравниваемых групп судят по разности выборочных средних. Так как значения выборочных средних (или других выборочных характеристик) являются случайными величинами, варьирующимися около значений параметров генеральной совокупности, то разница между сравниваемыми выборочными параметрами может возникнуть вследствие случайности, не из-за систематического воздействия на изучаемый признак. Установление значимости различия (является ли различие систематическим или случайным) осуществляется проверкой статистической гипотезы.
§5.1. Статистические гипотезы
Статистические гипотезы. Статистической гипотезой называется предположение о виде неизвестного распределения или о значениях параметров распределения наблюдаемых в эксперименте случайных величин. Нулевой (основной) называется выдвинутая гипотеза, которая обозначается Н 0. Альтернативной (конкурирующей) называется гипотеза, которая противоречит основной (обозначение: Н 1). Если производится сравнение одной выборки, генеральный параметр которой z 1, с другой выборкой, генеральный параметр которой z 2, то основная гипотеза формулируется обычно так: генеральные параметры сравниваемых выборок равны, то есть различия между выборочными параметрами носят не систематический, а исключительно случайный характер. Основную гипотезу принято записывать в виде: Н 0: z 1= z 2. Альтернативные гипотезы могут иметь один из следующих видов: а) Н 1: z 1> z 2; б) Н 1: z 1< z 2; в) Н 1: z 1¹ z 2. Гипотезы (а) и (б) называются направленными, а гипотеза вида (в) – ненаправленной. Проверка гипотезы позволяет сделать вывод о том, противоречит ли выдвинутая гипотеза эмпирическим данным, или нет. Нулевую гипотезу проверяют на основании данных выборки. В следствие случайности выборки возможны следующие виды ошибок: 1) ошибка первого рода имеет место тогда, когда отвергается правильная гипотеза; 2) ошибка второго рода имеет место тогда, когда принимается неправильная гипотеза. Вероятность совершить ошибку первого рода называется уровнем значимости a. В прикладных исследованиях обычно принимается уровень значимости a=0,05, и в особых случаях, требующих высокой точности, полагают a=0,01. Статистический критерий. Критические области. Статистическим критерием (или просто критерием) называется специально выработанная случайная величина К с известной функцией распределения, которая служит для проверки основной гипотезы. Значение критерия, вычисленное по выборке, называется наблюдаемым значением критерия и обозначается Критической областью называется множество значений критерия, при которых отвергается основная гипотеза. Границы критической области называются критическими точками kc. Виды критических областей: 1) правосторонняя: если К > kc; применяется, если Н 1: z 1> z 2; 2) левосторонняя: если К <- kc; применяется, если Н 1: z 1< z 2; 3) двусторонняя: если К < kc 1 и К > kc 2, причем kc 2> kc 1; применяется, если Н 1: z 1¹ z 2. (правосторонняя или левосторонняя область называется односторонней). Критерий Фишера. Для оценки значимости различия исправленных дисперсий Требуется проверить основную гипотезу Н 0: Наблюдаемое значение критерия Фишера вычисляется по формуле:
В числителе (4.1) всегда должна быть та дисперсия, которая больше! Критерий Стьюдента. Пусть из двух генеральных совокупностей Х и Y, имеющих распределение, близкое к нормальному, извлечено по одной независимой выборке. Вычисленные по этим выборкам средние значения Требуется проверить основную гипотезу Н 0: Наблюдаемое значение критерия Стьюдента вычисляется по формуле:
где величина · если объемы выборок nх и nу примерно одинаковые и достаточно большие, т.е. nх >30 и nу >30, то
где · если объемы выборок nх и nу малы, т.е. nх <30 и nу <30, а дисперсии генеральных совокупностей неизвестны и предполагаются равными, то
где Поэтому перед вычислением критерия Стьюдента всегда следует проверить гипотезу о равенстве генеральных дисперсий с помощью критерия Фишера. Глава 5. Проверка статистических гипотез
В научных исследованиях для доказательства достоверности результатов эксперимента необходимо оценивать их значимость. Приходится сравнивать данные опыта с контрольными данными, причем о преимуществе одной из сравниваемых групп судят по разности выборочных средних. Так как значения выборочных средних (или других выборочных характеристик) являются случайными величинами, варьирующимися около значений параметров генеральной совокупности, то разница между сравниваемыми выборочными параметрами может возникнуть вследствие случайности, не из-за систематического воздействия на изучаемый признак. Установление значимости различия (является ли различие систематическим или случайным) осуществляется проверкой статистической гипотезы.
§5.1. Статистические гипотезы
Статистические гипотезы. Статистической гипотезой называется предположение о виде неизвестного распределения или о значениях параметров распределения наблюдаемых в эксперименте случайных величин. Нулевой (основной) называется выдвинутая гипотеза, которая обозначается Н 0. Альтернативной (конкурирующей) называется гипотеза, которая противоречит основной (обозначение: Н 1). Если производится сравнение одной выборки, генеральный параметр которой z 1, с другой выборкой, генеральный параметр которой z 2, то основная гипотеза формулируется обычно так: генеральные параметры сравниваемых выборок равны, то есть различия между выборочными параметрами носят не систематический, а исключительно случайный характер. Основную гипотезу принято записывать в виде: Н 0: z 1= z 2. Альтернативные гипотезы могут иметь один из следующих видов: а) Н 1: z 1> z 2; б) Н 1: z 1< z 2; в) Н 1: z 1¹ z 2. Гипотезы (а) и (б) называются направленными, а гипотеза вида (в) – ненаправленной. Проверка гипотезы позволяет сделать вывод о том, противоречит ли выдвинутая гипотеза эмпирическим данным, или нет. Нулевую гипотезу проверяют на основании данных выборки. В следствие случайности выборки возможны следующие виды ошибок: 1) ошибка первого рода имеет место тогда, когда отвергается правильная гипотеза; 2) ошибка второго рода имеет место тогда, когда принимается неправильная гипотеза. Вероятность совершить ошибку первого рода называется уровнем значимости a. В прикладных исследованиях обычно принимается уровень значимости a=0,05, и в особых случаях, требующих высокой точности, полагают a=0,01.
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.104 (0.006 с.) |

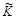 .
. и
и 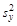 (пусть
(пусть  =
=  .
. . (4.1)
. (4.1)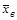 и
и  , как правило, различаются. В силу случайности выборки это различие может быть случайным, и генеральные средние
, как правило, различаются. В силу случайности выборки это различие может быть случайным, и генеральные средние  и
и 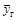 могут совпадать.
могут совпадать. , (4.3)
, (4.3) называется ошибкой разности выборочных средних. Вычисление
называется ошибкой разности выборочных средних. Вычисление  зависит от объемов выборок и того, предполагаются ли равными или нет неизвестные дисперсии генеральных совокупностей:
зависит от объемов выборок и того, предполагаются ли равными или нет неизвестные дисперсии генеральных совокупностей: ,
, и
и 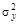 – дисперсии выборок из двух генеральных совокупностей Х и Y;
– дисперсии выборок из двух генеральных совокупностей Х и Y;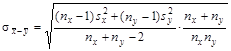 ,
, и
и  – исправленные дисперсии выборок из двух генеральных совокупностей Х и Y.
– исправленные дисперсии выборок из двух генеральных совокупностей Х и Y.


