
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила принятия решения при использовании критерия Стьюдента.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте 1) Если альтернативная гипотеза Н 1: k = nх + nу -2, (4.4) где nх и nу - объемы выборок, находится критическая точка двусторонней критической области t a(k). Это значение сравнивается с наблюдаемым значением критерия Стьюдента: · если · если 2) Если альтернативная гипотеза Н 1: · если · если
Сравнение средних двух независимых выборок в Excel. Наиболее быстрым и удобным способом проверки статистической гипотезы о равенстве средних в Excel является использование Пакета анализа. Поскольку критерий Стьюдента зависит от того, равны или нет дисперсии генеральных совокупностей, из которых произведены две независимые выборки, то для сравнения средних этих выборок, соответственно, имеется два инструмента анализа: Двухвыборочный t-тест с одинаковыми дисперсиями, Двухвыборочный t-тест с различными дисперсиями. Для вызова любого из данных инструментов анализа необходимо выполнить команду Сервис ® Анализ данных, а затем в появившемся диалоговом окне Анализ данных выбрать нужный вам инструмент. Естественно, что выбор t -теста можно осуществить, только после того, как произведена проверка гипотезы о равенстве генеральных дисперсий двух выборок и установлено с помощью критерия Фишера (F -теста), значимо ли различаются дисперсии выборок или нет. Если дисперсии выборок оказались равными, то следует выбрать инструмент Двухвыборочный t-тест с одинаковыми дисперсиями. После нажатия на кнопку ОК появится диалоговое окно с названием выбранного инструмента анализа. Вид этого окна:
Порядок ввода данных в этом окне точно такой же, как и в диалоговом окне инструмента анализа Двухвыборочный F-тест для дисперсии. В окне t -теста имеется поле гипотетическая разность средних, в которое при необходимости можно ввести предполагаемую разность генеральных средних. Обычно это поле оставляют незаполненным, что соответствует о том, что проверяется нулевая гипотеза о равенстве генеральных средних Н 0: Переключатель Метки следует активизировать в том случае, если диапазон ячеек с входными данными содержит в первой строке заголовок. Поскольку, обычно во входных данных указываются адреса ячеек с результатами измерений, то переключатель Метки лучше не активизировать. После заполнения необходимых полей диалогового окна Двухвыборочный t-тест с одинаковыми дисперсиями и нажатия на ОК появится таблица с таким же названием. В появившейся таблице будут содержаться вычисленные средние и дисперсии для каждой выборки, объемы этих выборок (в строке: Наблюдения), теоретическая генеральная дисперсия обеих выборок (в строке: Объединенная дисперсия), число степеней свободы распределения Стьюдента (4.4) (в строке: df), наблюдаемое значение критерия Стьюдента (4.3) (в строке: t-статистика), вероятность того, что наблюдаемое значение критерия Стьюдента будет меньше или равно критической точке распределения Стьюдента правосторонней критической области (в строке: P(T<=t) одностороннее); критическая точка распределения Стьюдента для заданного уровня значимости a правосторонней критической области (в строке: t критическое одностороннее); вероятность того, что наблюдаемое значение критерия Стьюдента будет меньше или равно критической точке распределения Стьюдента двусторонней критической области (в строке: P(T<=t) двустороннее); критическую точку распределения Стьюдента двусторонней критической области (в строке: t критическое двустороннее). Если после выполнения F -теста дисперсии выборок оказались различными, то следует выбрать инструмент Двухвыборочный t-тест с различными дисперсиями. После нажатия на кнопку ОК появится диалоговое окно с названием выбранного инструмента. Порядок заполнения полей в этом диалоговом окне точно такой же как и в предыдущем случае. Вычисляемая в t -тесте с различными дисперсиями таблица практически совпадает с таблицей, вычисляемой в t -тесте с одинаковыми дисперсиями, за исключением того, что в таблице t -теста с различными дисперсиями нет строки объединенная дисперсия. Эти тесты для средних вычисляют различные значения критериев Стьюдента в тех случаях, когда дисперсии выборок отличаются существенно. Если дисперсии одинаковы, то оба теста вычисляют одинаковые значения. Для принятия решения следует сравнить наблюдаемое значение критерия Стьюдента, находящееся в строке t-статистика, с критической точкой распределения Стьюдента двухсторонней критической области, находящейся в строке t критическое двухстороннее, если альтернативная гипотеза Н 1:
|
||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |

 ¹
¹ 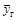 , то по таблице критических точек распределения Стьюдента (или вычисляется в Excel) для заданного уровня значимости a и числа степеней свободы распределения Стьюдента, равного
, то по таблице критических точек распределения Стьюдента (или вычисляется в Excel) для заданного уровня значимости a и числа степеней свободы распределения Стьюдента, равного < t a(k), то нет оснований отвергнуть основную гипотезу, то есть различие между выборочными средними признается случайным и экспериментальные данные не противоречат предположению о равенстве генеральных средних;
< t a(k), то нет оснований отвергнуть основную гипотезу, то есть различие между выборочными средними признается случайным и экспериментальные данные не противоречат предположению о равенстве генеральных средних;



