
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критериальный язык описания выбораСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Принятие решений (ВЫБОР)
Будем представлять принятие решения как действие над множеством альтернатив, в результате которого получается подмножество выбранных альтернатив (обычно это одна альтернатива, что не обязательно, а иногда и невозможно). Последствия выбора могут быть точно известны (выбор в условиях определенности ), иметь вероятностный характер, когда известны вероятности возможных исходов после сделанного выбора (выбор в условиях риска ), или иметь неоднозначный исход, не допускающий введения вероятностей (выбор в условиях неопределенности) Три основных языка описания выбора: · критериальный язык, · язык бинарных отношений, · язык функций выбора. КРИТЕРИАЛЬНЫЙ ЯЗЫК ОПИСАНИЯ ВЫБОРА
Пусть Если теперь сделать еще одно важное предположение, что выбор любой альтернативы приводит к однозначно известным последствиям (т.е. считать, что выбор осуществляется в условиях определенности) и заданный критерий
Задачи (1), связанные с нахождением минимума или максимума критерия
Оптимизация (выбор) в экономическом анализе
а)Простейшая модель фирмы
Предполагается, что ресурсы доступны, а продукт может быть продан в любом количестве.
Рациональное экономическое поведение – выбор объемов ресурсов и выпуска продукции на основе максимизации прибыли
Задача: нахождение таких неотрицательных величин используемых объемов ресурсов
Задача безусловной оптимизации (задача без ограничений)
Задача условной оптимизации (задача с ограничениями или задача математического Программирования)
Задача безусловной оптимизации Постановка и схема решения задачи
Данные: Модель:
Задача безусловной оптимизации имеет вид:
Предполагается, что функция
и матрицу Гессе
Схема решения задачи оптимизации может выглядеть следующим образом: 1. Находятся все точки локальных минимумов; 2. Вычисляются значения функции
Необходимые и достаточные условия наличия локального экстремума
Теорема 1 Необходимое условие наличия локального экстремума Пусть
Точка
Для выявления искомой точки на множестве стационарных используется условие локальной оптимальности второго порядка Теорема 2 Пусть
где
Теорема 3 Достаточное условие локальной оптимальности
Пусть
то
Введение
В зависимости от ситуации под запасами могут подразумеваться: готовая продукция, сырье, полуфабрикаты, станки, инструмент, транспортные средства, наличные деньги и др.
При управлении запасами принимаются решения:
· когда закупать необходимые ресурсы (пополнять запас); · какое количество продукции заказывать? (каков должен быть размер заказываемой партии).
Затраты при организации запасов товаров: · затраты, связанные с выполнением заказа – расходы по оформлению заказа, транспортные расходы, затраты на обработку заказов и ведение учета поставок и др.; · затраты, связанные с хранением товаров; · потери от дефицита; · затраты на приобретение товаров
Суммарные затраты =
Факторы, учитываемые при построении модели: спрос на данный товар; запаздывание поставки заказа или срок выполнения заказа; как происходит пополнение запаса; горизонт планирования; номенклатура запасаемых товаров.
Градиентные методы поиска Методы используют информацию о градиенте целевой функции и относятся к методам первого порядка.
Поскольку
Из свойства скалярного произведения
градиентные методы
Методы спуска
1. Простейший градиентный метод 2. Метод наискорейшего спуска
Из (11) следует:
3. Градиентный метод с дроблением шага 3.1.
3.2.
Вычислительная процедура
1.
2.
3.
4.
5. Проверка условий останова: если выполняются иначе к п. 2
Особенности методов: · относятся к локальным методам оптимизации; · используются для решения как одномерных, так и многомерных экстремальных задач; · выпуклая ЦФ – метод сходится к точке минимума; сильно выпуклая ЦФ - метод сходится к точке минимума с линейной скоростью; невыпуклая ЦФ - метод сходится ко множеству стационарных точек · градиентные методы относятся к методам спуска · низкая скорость сходимости в окрестности точки минимума; метод чувствителен к ошибкам вычислений; градиентные методы целесообразно применять на начальном этапе оптимизационной процедуры.
Метод Ньютона
(1)
Процедура поиска
Из (1) имеем
(3) в (2)
- оптимизационный метод Ньютона
Особенности метода Ньютона
1. Трудоемкость, обусловленная вычислением и обращением матрицы Гессе на каждой итерации; 2. Выбор 3. Метод Ньютона сходится к точке минимума произвольной ЦФ с квадратичной скоростью, если матрица Гессе
Метод Ньютона с регулировкой шага:
Скорость сходимости – сверхлинейная; квадратичная
Постановка задачи Пример. Рассмотрим поведение фирмы в долгосрочном периоде, когда все используемые факторы являются переменными. Здесь предприятие сталкивается с проблемой выбора факторов, обеспечивающих достижение некоторого заданного объема производства Будем считать, что для производства продукта в объеме Y 0 используются два фактора труд L и капитал K, связанные с выпуском производственной функцией
C=WL+RK ®min при ограничении на объем выпуска Y 0
F(K,L)= Y0 и условии положительных переменных K>0, L>0, что следует из свойства производственной функции. Данная задача представляет собой задачу нелинейного программирования C=WL+RK ®min, F(K,L)= Y0, K>0, L>0. В общем случае в задачах нелинейного программирования допустимое множество
Ограничений на m здесь нет. Хотя бы одно из ограничений имеет вид неравенства. Хотя бы одна из функций – нелинейная. В векторной форме задача нелинейного программирования принимает вид:
Определение 1 Ограничения вида
или
называются функциональными ограничениями. Ограничения вида
называются прямыми ограничениями.
Определение 2 Ограничение - неравенство
будем называть активным (эффективным) в точке
В противном случае ограничение будем называть неактивным (неэффективным)
УСЛОВНАЯ МАКСИМИЗАЦИЯ
при условии, что дополнительные критерии остаются на заданных им уровнях. На рис. 7.1,6 приведено решение задачи
В некоторых задачах оказывается возможным или даже необходимым задавать ограничения на сопутствующие критерии не столь жестко, как в задаче (7). Например, если сопутствующий критерий характеризует стоимость затрат, то вместо фиксации затрат разумнее задавать их верхний уровень, т.е. формулировать задачу с ограничениями типа неравенств:
На рис. приведено решение задачи
Принятие решений (ВЫБОР)
Будем представлять принятие решения как действие над множеством альтернатив, в результате которого получается подмножество выбранных альтернатив (обычно это одна альтернатива, что не обязательно, а иногда и невозможно). Последствия выбора могут быть точно известны (выбор в условиях определенности ), иметь вероятностный характер, когда известны вероятности возможных исходов после сделанного выбора (выбор в условиях риска ), или иметь неоднозначный исход, не допускающий введения вероятностей (выбор в условиях неопределенности) Три основных языка описания выбора: · критериальный язык, · язык бинарных отношений, · язык функций выбора. КРИТЕРИАЛЬНЫЙ ЯЗЫК ОПИСАНИЯ ВЫБОРА
Пусть Если теперь сделать еще одно важное предположение, что выбор любой альтернативы приводит к однозначно известным последствиям (т.е. считать, что выбор осуществляется в условиях определенности) и заданный критерий
Задачи (1), связанные с нахождением минимума или максимума критерия
|
||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.152 (0.009 с.) |

 — некоторая альтернатива из множества X. Считается, что для всех
— некоторая альтернатива из множества X. Считается, что для всех  может быть задана функция
может быть задана функция  , которая называется критерием (критерием качества, целевой функцией, функцией предпочтения, функцией полезности и т.д.) и обладает тем свойством, что если альтернатива
, которая называется критерием (критерием качества, целевой функцией, функцией предпочтения, функцией полезности и т.д.) и обладает тем свойством, что если альтернатива  предпочтительнее альтернативы
предпочтительнее альтернативы  (будем обозначать это
(будем обозначать это  ),
),  и обратно.
и обратно. численно выражает оценку этих последствий, то наилучшей альтернативой
численно выражает оценку этих последствий, то наилучшей альтернативой  является, естественно, та, которая обладает наибольшим (или наименьшим) значением критерия:
является, естественно, та, которая обладает наибольшим (или наименьшим) значением критерия: .
. 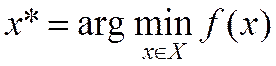 (1)
(1) – затраты
– затраты  - производственного ресурса,
- производственного ресурса,  ,в течение некоторого периода времени,
,в течение некоторого периода времени,  .
. – производственная функция, связывающая объем производимого продукта
– производственная функция, связывающая объем производимого продукта  с объемами используемых ресурсов;
с объемами используемых ресурсов; – цена продукта,
– цена продукта, – заданные цены ресурсов.
– заданные цены ресурсов. (2)
(2) - выручка от реализации продукции;
- выручка от реализации продукции; - затраты, связанные с производством продукта.
- затраты, связанные с производством продукта. , при которых
, при которых (2а)
(2а) (6)
(6) (7)
(7)
 ;
; ;
; - управляющие переменные;
- управляющие переменные;
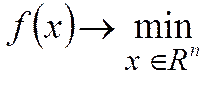 (6)
(6) дважды непрерывно дифференцируема всюду на
дважды непрерывно дифференцируема всюду на  , т.е. в точке
, т.е. в точке  имеет градиент
имеет градиент
 .
. во всех найденных точках и выбирается точка с наименьшим значением функции. Это и есть решение задачи.
во всех найденных точках и выбирается точка с наименьшим значением функции. Это и есть решение задачи. - непрерывно дифференцируемая функция в точке
- непрерывно дифференцируемая функция в точке  - точка локального минимума (максимума) функции
- точка локального минимума (максимума) функции  (7)
(7) , удовлетворяющая условию (7), называется стационарной точкой функции
, удовлетворяющая условию (7), называется стационарной точкой функции  - дважды непрерывно дифференцируемая функция в некоторой окрестности точки
- дважды непрерывно дифференцируемая функция в некоторой окрестности точки  , (8)
, (8)
 , (9)
, (9) (3)
(3)  дифференцируема на
дифференцируема на 



 (4)
(4) 
 (5)
(5)  , то
, то  (6)
(6)
 (7)
(7)
 . (8)
. (8) - (9)
- (9) ,
, (10)
(10)  ;
; (11)
(11)

 часто
часто  ;
; к следующей итерации
к следующей итерации
 ,
, ,
, ,
,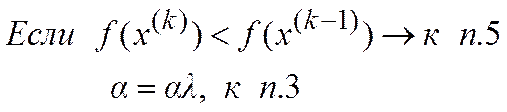
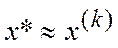 ;
; ;
;



 (2)
(2)

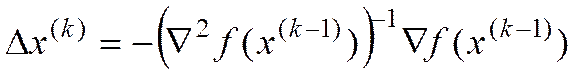 , (3)
, (3)  (4)
(4)  ;
; положительно определена, а
положительно определена, а  располагается «достаточно близко» к
располагается «достаточно близко» к  .
.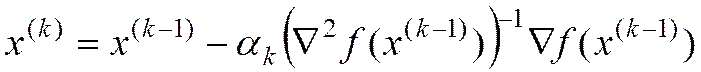 (5)
(5)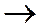
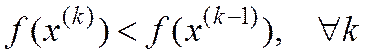
 ,
,
 с минимальными затратами.
с минимальными затратами. и нанятые (или арендованные) на конкурентных рынках по фиксированным ценам. Цена труда равна номинальной ставке заработной платы W, а цена капитала – арендной плате за оборудование R. Предполагаем также, что факторы производства K и L характеризуются предельным продуктом капитала g =¶ F (K,L)/¶ K >0 и предельным продуктом труда v =¶ F (K,L)/¶ L >0. Тогда проблема оптимального выбора факторов сводится к задаче минимизации совокупных затрат
и нанятые (или арендованные) на конкурентных рынках по фиксированным ценам. Цена труда равна номинальной ставке заработной платы W, а цена капитала – арендной плате за оборудование R. Предполагаем также, что факторы производства K и L характеризуются предельным продуктом капитала g =¶ F (K,L)/¶ K >0 и предельным продуктом труда v =¶ F (K,L)/¶ L >0. Тогда проблема оптимального выбора факторов сводится к задаче минимизации совокупных затрат представляет собой множество решений систем алгебраических уравнений и неравенств (ограничения – равенства, ограничения - неравенства):
представляет собой множество решений систем алгебраических уравнений и неравенств (ограничения – равенства, ограничения - неравенства): , (1)
, (1)
 (2)
(2) . ()
. ()



 , если
, если .
. (7)
(7) .
.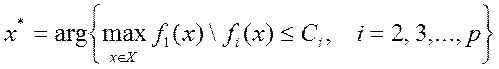 . (8)
. (8) .
.


