
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимые условия локального минимумаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
(условия Куна-Таккера)
Условия Куна – Таккера :
Выводы: Замечание 1. Если ограничение – неравенство имеет вид
Замечание 2. Если выпуклая целевая функция определена на выпуклом допустимом множестве
Решим сформулированную выше задачу нелинейного программирования C=WL+RK ®min, F(K,L)= Y0, K>0, L>0.
Для решения задачи воспользуемся необходимыми условиями оптимальности Куна - Таккера, записанными в терминах функции Лагранжа. Функция Лагранжа в данном случае принимает вид (20) где l - множитель Лагранжа. Определяя частные производные этой функции по K, L и l и приравнивая полученные выражения к нулю, получим необходимые условия минимума для положительных объемов факторов K >0, L >0
(21) Решение данной системы K, L находится для конкретного вида производственной функции. Вместе с тем можно сформулировать правило, согласно которому выбор факторов считается оптимальным, т.е. минимизирующим издержки. Определим множитель Лагранжа из первых двух соотношений (21), обозначая предельные продукты через g и v
(22)
Предположим, что выпуск увеличился на одну единицу. Так как предельный продукт капитала g=DY/DK показывает дополнительный объем выпуска, получаемый при использовании дополнительной единицы капитала, то 1/ g =D K /D Y измеряет дополнительный капитал, необходимый для производства единицы продукта. Следовательно, величина R/g соответствует дополнительным затратам на производство единицы продукции за счет увеличения капитала, т.е. предельным затратам производства относительно переменного фактора K. Аналогично величина W/v показывает предельные затраты производства относительно переменного фактора L.
Таким образом, фирма минимизирует производственные затраты при выпуске продукции, если она выбирает такое сочетание факторов, при котором предельные затраты относительно этих факторов равны (22) или соблюдается равенство предельных продуктов факторов, отнесенных к цене соответствующего фактора g/ R=v/W.
Задача линейного программирования ( см. файл ЛП)
Выбор с несколькими критериями Пример. Формирование инвестиционного портфеля
Итак, пусть для оценивания альтернатив используется несколько критериев
СВЕДЕНИЕ МНОГОКРИТЕРИАЛЬНОЙ ЗАДАЧИ К ОДНОКРИТЕРИАЛЬНОЙ Введение суперкритерия, т.е. скалярной функции векторного аргумента
Суперкритерий позволяет упорядочить альтернативы по величине f0,выделив тем самым наилучшую (в смысле этого критерия).
Коэффициенты
УСЛОВНАЯ МАКСИМИЗАЦИЯ
при условии, что дополнительные критерии остаются на заданных им уровнях. На рис. 7.1,6 приведено решение задачи
В некоторых задачах оказывается возможным или даже необходимым задавать ограничения на сопутствующие критерии не столь жестко, как в задаче (7). Например, если сопутствующий критерий характеризует стоимость затрат, то вместо фиксации затрат разумнее задавать их верхний уровень, т.е. формулировать задачу с ограничениями типа неравенств:
На рис. приведено решение задачи
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 539; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.226 (0.009 с.) |



 ()
() , то его необходимо вводить в функцию Лагранжа в форме
, то его необходимо вводить в функцию Лагранжа в форме 
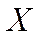 , то необходимые условия оптимальности Куна – Таккера являются одновременно и достаточными.
, то необходимые условия оптимальности Куна – Таккера являются одновременно и достаточными.

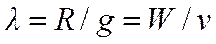

 . Теоретически можно представить себе случай, когда во множестве X окажется одна альтернатива, обладающая наибольшими значениями всех
. Теоретически можно представить себе случай, когда во множестве X окажется одна альтернатива, обладающая наибольшими значениями всех  критериев; она и является наилучшей. Однако на практике такие случаи почти не встречаются, и возникает вопрос, как же тогда осуществлять выбор (так, например, на рис. 7.1 множеству X соответствуют внутренние точки фигуры на плоскости значении двух критериев
критериев; она и является наилучшей. Однако на практике такие случаи почти не встречаются, и возникает вопрос, как же тогда осуществлять выбор (так, например, на рис. 7.1 множеству X соответствуют внутренние точки фигуры на плоскости значении двух критериев  ; оба критерия желательно максимизировать).
; оба критерия желательно максимизировать).
 .
.
 обеспечивают безразмерность числа
обеспечивают безразмерность числа  (частные критерии могут иметь разную размерность, и тогда некоторые арифметические операции над ними, например сложение, не имеют смысла). Коэффициенты
(частные критерии могут иметь разную размерность, и тогда некоторые арифметические операции над ними, например сложение, не имеют смысла). Коэффициенты  отражают относительный вклад частных критериев в суперкритерий.
отражают относительный вклад частных критериев в суперкритерий. .
. (7)
(7) .
.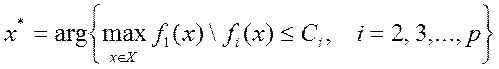 . (8)
. (8) .
.


