
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая постановка задачи оптимизацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Рассмотренные выше задачи принято называть задачами статической оптимизации. Основными понятиями статической оптимизации являются понятия целевой функции, управляющих переменных, допустимого множества и параметров задачи. Рассмотрим эти понятия. Целевая функция) – это функция, соответствующая критерию качества. ЦФ представляет собой функцию многих переменных, с помощью которой дается математическое изложение цели задачи. Целевая функция обычно представляется в виде
где В задаче оптимизации принято различать два типа переменных – управляющие переменные и параметры задачи. Под управляющими переменными понимаются те переменные модели, изменение которых приводит к достижению цели, т.е. к достижению максимального (минимального) значения целевой функции. Наоборот, параметры задачи не могут быть использованы для увеличения значения целевой функции – они либо заданы, либо являются неопределенными (последнее значительно усложняет решение задачи оптимизации). В примере управляющими переменными являются величины потребления ресурсов
Целевой функцией является прибыль
В рамках данного курса будут рассматриваться исключительно так называемые детерминированные задачи оптимизации, то есть задачи с заданными значениями параметров.
В общем случае, если вектор управляющих переменных х удовлетворяет ограничениям задачи, он называется допустимым, а множество всех допустимых векторов образует допустимое множество решений X. Допустимое множество является подмножеством
Так как задача заключается в выборе вектора управляющих переменных из допустимого множества, то в любой нетривиальной задаче оно является непустым и содержит, по крайней мере, две различные точки (два решения). В этом случае можно сформулировать задачу минимизации (максимизации).
Задача минимизации состоит в поиске такого вектора управляющих переменных из допустимого множества
Определение. Точка
f (х*)
Определение. Точка х*ÎX называется точкой строгого локального минимума функции
f (х*) < f (х) при всех
Глобальный минимум функции
f (х*) ≤ f (х) при всех х Î X,
Строгий глобальный минимум функции
f (х*) < f (х) при всех х Î X,
Решение задачи сводится к поиску конечного числа
Сделаем несколько терминологических замечаний.
Замечание 1. В теории и методах оптимизации часто используется понятие э кстремума. Экстремум – это обобщающее понятие для максимума и минимума, которое означает максимум в задачах максимизации и минимум в задачах минимизации. Точка экстремума – это точка, в которой целевая функция достигает экстремума. Различают точки глобального экстремума и локального экстремума. Точка глобального экстремума всегда является также и точкой локального экстремума. Обратное неверно. Экстремальное значение – это значение целевой функции в экстремальной точке.
Замечание 2. Задачу оптимизации с ограничениями на управляющие переменные называют задачей условной оптимизации, а максимум (минимум) в рассматриваемой задаче называют условным.
Замечание 3. Целевая функция
Замечание 4. Вектор управляющих переменных часто называют вектором решений или вектором управлений.
Виды экстремумов 1) максимум или минимум; 2) локальный или глобальный; 3) условный или безусловный; 4) строгий или нестрогий; 5) внутренний или граничный (краевой); Внутренний экстремум – это такой максимум или минимум, который достигается во внутренней точке множества
|
||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1003; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |

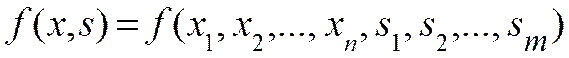 , (3)
, (3) – переменные задачи.
– переменные задачи. , а параметрами задачи являются цены ресурсов и продукта, то есть величины
, а параметрами задачи являются цены ресурсов и продукта, то есть величины 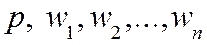 .
. .
. .
.
 .
. , при котором целевая функция принимает минимальное значение:
, при котором целевая функция принимает минимальное значение: или
или 

 на множестве
на множестве  , если
, если  и соответствующая
и соответствующая  -окрестность
-окрестность  точки
точки  такие, что
такие, что f (х) при всех
f (х) при всех  (4)
(4) на множестве
на множестве  , если
, если  и соответствующая
и соответствующая  -окрестность
-окрестность  точки
точки 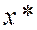 такие, что
такие, что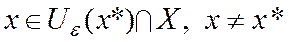 . (5)
. (5) на множестве
на множестве 

 на множестве
на множестве 
 переменных
переменных  на множестве
на множестве  , при которых ЦФ достигает минимального (экстремального) значения. Такие задачи называются конечномерными экстремальными или оптимизационными задачами.
, при которых ЦФ достигает минимального (экстремального) значения. Такие задачи называются конечномерными экстремальными или оптимизационными задачами.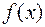 часто называется критерием оптимизации, поскольку является критерием выбора того или иного вектора хÎX.
часто называется критерием оптимизации, поскольку является критерием выбора того или иного вектора хÎX. . Граничный (краевой) экстремум достигается на границе множества
. Граничный (краевой) экстремум достигается на границе множества 


