
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основная модель управления запасамиСодержание книги Поиск на нашем сайте
Наиболее простой является так называемая основная модель управления запасами (модель Уилсона, система с фиксированным размером заказа)
Допущения модели Уилсона
Годовой спрос является априорно известной и постоянной величиной, интенсивность спроса время поставки заказа является известной и постоянной величиной каждый заказ поставляется в виде одной партии; затраты на осуществление заказа не зависят от размера заказа; Отсутствие запаса является недопустимым (дефицит отсутствует).
Средний уровень запасов
Годовые затраты на выполнение заказов
Затраты, связанные с хранением продукции
Если
Если
Общие сведения о численных методах оптимизации Определение 1. Численный метод - это правило (алгоритм), в соответствии с которым вычисляется последовательность величин Правило формирования последовательности
Вектор
число
Если используется информация только о целевой функции
Если алгоритм за конечное число шагов приводит в точку
Алгоритм (1) относят к методам спуска
(2) 2.5. Алгоритмы многомерной оптимизации
Градиентные методы поиска Методы используют информацию о градиенте целевой функции и относятся к методам первого порядка.
Поскольку
Из свойства скалярного произведения
градиентные методы
Методы спуска
1. Простейший градиентный метод 2. Метод наискорейшего спуска
Из (11) следует:
3. Градиентный метод с дроблением шага 3.1.
3.2.
Вычислительная процедура
1.
2.
3.
4.
5. Проверка условий останова: если выполняются иначе к п. 2
Особенности методов: · относятся к локальным методам оптимизации; · используются для решения как одномерных, так и многомерных экстремальных задач; · выпуклая ЦФ – метод сходится к точке минимума; сильно выпуклая ЦФ - метод сходится к точке минимума с линейной скоростью; невыпуклая ЦФ - метод сходится ко множеству стационарных точек · градиентные методы относятся к методам спуска · низкая скорость сходимости в окрестности точки минимума; метод чувствителен к ошибкам вычислений; градиентные методы целесообразно применять на начальном этапе оптимизационной процедуры.
Методы сопряженных направлений
а)
Определение. Пусть
Тогда совокупность векторов
Определение. Алгоритм
при (13) называется методом сопряженных направлений
Утверждение
Тогда (14) в случае (12) при условии (15) и произвольном
Формирование системы сопряженных направлений
б) ЦФ не является квадратичной
1.
2. Проверка выполнения условий останова: Условия выполняются
Условия не выполняются
Идти к п.1
При этом
Метод сопряженных градиентов (метод Ривса), метод первого порядка
в) Лемма.
точки минимума функции
при поиске вдоль направления
Тогда вектор
Рис. 1
Метод Ньютона
(1)
Процедура поиска
Из (1) имеем
(3) в (2)
- оптимизационный метод Ньютона
Особенности метода Ньютона
1. Трудоемкость, обусловленная вычислением и обращением матрицы Гессе на каждой итерации; 2. Выбор 3. Метод Ньютона сходится к точке минимума произвольной ЦФ с квадратичной скоростью, если матрица Гессе
Метод Ньютона с регулировкой шага:
Скорость сходимости – сверхлинейная; квадратичная
|
||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.148.189 (0.009 с.) |

 ;
; ;
; ;
; - размер заказываемой партии продукции
- размер заказываемой партии продукции



 - затраты на выполнение заказа
- затраты на выполнение заказа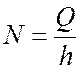 - число заказов в год
- число заказов в год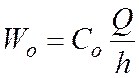

 - ставка процента,
- ставка процента, - цена единицы товара
- цена единицы товара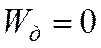
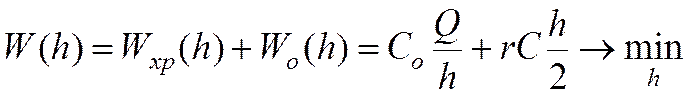

 - формула Уилсона
- формула Уилсона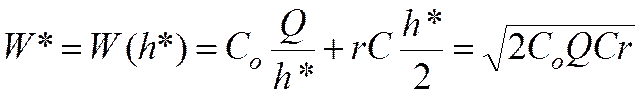
 ,
, 

 - точка заказа;
- точка заказа; , - точка заказа;
, - точка заказа; , которая должна сходиться к решению оптимизационной задачи
, которая должна сходиться к решению оптимизационной задачи  .
.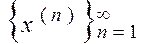
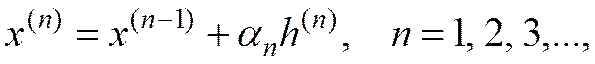 (1)
(1)  задает направление движения в пространстве
задает направление движения в пространстве 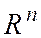 ,
, - величину "шага" при переходе из точки
- величину "шага" при переходе из точки  в точку
в точку  .
. , алгоритм называют алгоритмом нулевого порядка; если используется информация о производных первого порядка - алгоритмом первого порядка; если используются вторые производные - алгоритмом второго порядка и т.д.
, алгоритм называют алгоритмом нулевого порядка; если используется информация о производных первого порядка - алгоритмом первого порядка; если используются вторые производные - алгоритмом второго порядка и т.д. , его называют конечношаговым, иначе - бесконечношаговым.
, его называют конечношаговым, иначе - бесконечношаговым.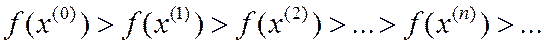 (3)
(3)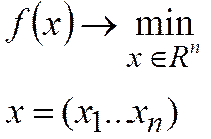 (1)
(1) (3)
(3)  дифференцируема на
дифференцируема на 



 (4)
(4) 
 (5)
(5)  , то
, то  (6)
(6)
 (7)
(7)
 . (8)
. (8) - (9)
- (9) ,
, (10)
(10)  ;
; (11)
(11)

 часто
часто  ;
; к следующей итерации
к следующей итерации
 ,
, ,
, ,
,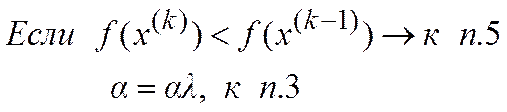
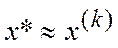 ;
; ;
; - квадратичная ЦФ
- квадратичная ЦФ 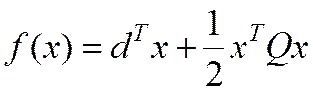 (12)
(12) - система
- система 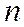 линейно независимых векторов,
линейно независимых векторов,  - симметрическая неотрицательно определенная
- симметрическая неотрицательно определенная  матрица; при этом выполняются условия
матрица; при этом выполняются условия (13)
(13) называется системой сопряженных направлений относительно матрицы
называется системой сопряженных направлений относительно матрицы  , (14)
, (14)  (15)
(15)  за
за  шагов обеспечивает достижение точки минимума (12), т.е.
шагов обеспечивает достижение точки минимума (12), т.е. 
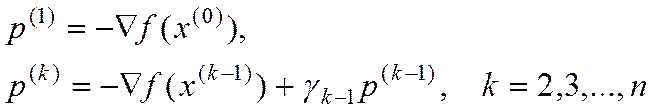 (16)
(16)

 (17)
(17)
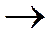
 ;
;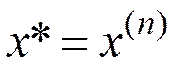
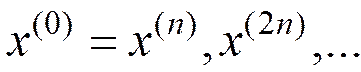
 (18)
(18)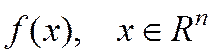
 - подпространства;
- подпространства;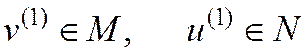 ;
; -
- в подпространствах
в подпространствах 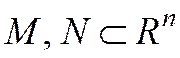
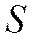 .
. сопряжен с направлением
сопряжен с направлением 
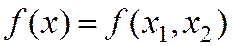






 (2)
(2)

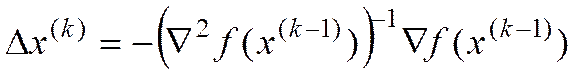 , (3)
, (3)  (4)
(4)  ;
; положительно определена, а
положительно определена, а  располагается «достаточно близко» к
располагается «достаточно близко» к  .
.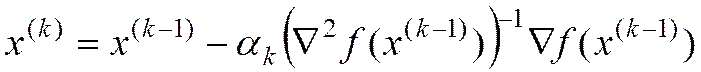 (5)
(5)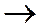
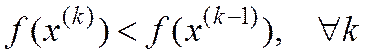
 ,
,



