
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача безусловной оптимизации (задача без ограничений)Содержание книги
Поиск на нашем сайте
Задача условной оптимизации (задача с ограничениями или задача математического Программирования)
Задача безусловной оптимизации Постановка и схема решения задачи
Данные: Модель:
Задача безусловной оптимизации имеет вид:
Предполагается, что функция
и матрицу Гессе
Схема решения задачи оптимизации может выглядеть следующим образом: 1. Находятся все точки локальных минимумов; 2. Вычисляются значения функции
Необходимые и достаточные условия наличия локального экстремума
Теорема 1 Необходимое условие наличия локального экстремума Пусть
Точка
Для выявления искомой точки на множестве стационарных используется условие локальной оптимальности второго порядка Теорема 2 Пусть
где
Теорема 3 Достаточное условие локальной оптимальности
Пусть
то
Знакоопределенность матрицы. Критерий Сильвестра Для установления знакоопределенности квадратной матрицы 1. Если знаки всех угловых миноров матрицы 2. Если знаки угловых миноров чередуются, начиная с минуса, то матрица
2.4. Одномерная минимизация
Для функции одной переменной
Достаточное условие
Модель спроса на наличные деньги
Согласно этой модели определяются размеры необходимой суммы наличных денег. Предполагается, что годовая потребность (годовой спрос) в наличных деньгах субъекта, которые находятся на банковском счете под процент
Рис.1
Средний уровень денег на руках
Годовые затраты на банковские операции
Альтернативные потери от хранения денег «на руках» (недополучение банковского процента)

Рис.2
Принятие решений в задаче управления запасами
Введение
В зависимости от ситуации под запасами могут подразумеваться: готовая продукция, сырье, полуфабрикаты, станки, инструмент, транспортные средства, наличные деньги и др.
При управлении запасами принимаются решения:
· когда закупать необходимые ресурсы (пополнять запас); · какое количество продукции заказывать? (каков должен быть размер заказываемой партии).
Затраты при организации запасов товаров: · затраты, связанные с выполнением заказа – расходы по оформлению заказа, транспортные расходы, затраты на обработку заказов и ведение учета поставок и др.; · затраты, связанные с хранением товаров; · потери от дефицита; · затраты на приобретение товаров
Суммарные затраты =
Факторы, учитываемые при построении модели: спрос на данный товар; запаздывание поставки заказа или срок выполнения заказа; как происходит пополнение запаса; горизонт планирования; номенклатура запасаемых товаров.
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 334; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.162.189 (0.009 с.) |

 (6)
(6) (7)
(7)
 ;
; ;
; - управляющие переменные;
- управляющие переменные;
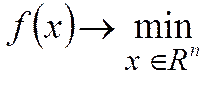 (6)
(6) дважды непрерывно дифференцируема всюду на
дважды непрерывно дифференцируема всюду на  , т.е. в точке
, т.е. в точке  имеет градиент
имеет градиент
 .
.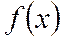 во всех найденных точках и выбирается точка с наименьшим значением функции. Это и есть решение задачи.
во всех найденных точках и выбирается точка с наименьшим значением функции. Это и есть решение задачи.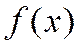 - непрерывно дифференцируемая функция в точке
- непрерывно дифференцируемая функция в точке  - точка локального минимума (максимума) функции
- точка локального минимума (максимума) функции  (7)
(7) , удовлетворяющая условию (7), называется стационарной точкой функции
, удовлетворяющая условию (7), называется стационарной точкой функции  - дважды непрерывно дифференцируемая функция в некоторой окрестности точки
- дважды непрерывно дифференцируемая функция в некоторой окрестности точки  , (8)
, (8)
 , (9)
, (9) предлагается следующая схема:
предлагается следующая схема: ;
; ;
;
 необходимые условия локальной оптимальности определяется следующими соотношениями:
необходимые условия локальной оптимальности определяется следующими соотношениями: (1)
(1)
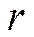 , известна -
, известна -  . При необходимости субъект посещает банк и снимает со счета определенную сумму денег -
. При необходимости субъект посещает банк и снимает со счета определенную сумму денег -  , которую он использует для покрытия своих расходов. Его запас наличности становится
, которую он использует для покрытия своих расходов. Его запас наличности становится  , а затем начинает уменьшаться с интенсивностью
, а затем начинает уменьшаться с интенсивностью  . Когда денежный запас исчерпан
. Когда денежный запас исчерпан  , следует новое обращение в банк и т.д. Графически эту процедуру можно представить следующим образом
, следует новое обращение в банк и т.д. Графически эту процедуру можно представить следующим образом



 - комиссионные расходы, связанные с однократным заказом денег в банке
- комиссионные расходы, связанные с однократным заказом денег в банке - число посещений банка в год
- число посещений банка в год



 - формула Баумоля – Тобина
- формула Баумоля – Тобина




