
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило принятия решения при использовании модифицированного критерия Стьюдента.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
По таблице критических точек распределения Стьюдента (или вычисляется в Excel) для заданного уровня значимости a и числа степеней свободы распределения Стьюдента, равного k = n -1, (4.7) находится критическая точка двусторонней критической области t a(k). Это значение сравнивается с наблюдаемым значением критерия · если · если
Сравнение средних двух зависимых выборок в Excel. Проверка значимости различия между результатами попарно зависимых измерений по модифицированному критерию Стьюдента (4.5) осуществляется в Excel с помощью инструмента анализа Парный двухвыборочный t-тест для средних. Для его вызова следует выполнить команду Сервис ® Анализ данных. В появившемся диалоговом окне Анализ данных выбрать инструмент Парный двухвыборочный t-тест для средних и нажать ОК. В появившемся диалоговом окне с названием выбранного инструмента анализа порядок заполнения точно такой же, как и в диалоговых окнах для t-тестов независимых выборок, описанных в предыдущем параграфе. После заполнения всех необходимых полей этого окна и нажатия на кнопку ОК появится таблица с названием Парный двухвыборочный t-тест для средних,в которой будут содержаться результаты вычислений. Данный тест вычисляет средние и дисперсии обеих выборок, их объемы, коэффициенты корреляции (в строке: Корреляция Пирсона), число степеней свободы (4.7) (в строке: df), наблюдаемое значение модифицированного критерия Стьюдента (4.5) (в строке: t-статистика), остальные строки называются также как и в таблицах t -тестов независимых выборок, описанных в предыдущем параграфе. Вычисленное в этом тесте наблюдаемое значение критерия (4.5), находящееся в строке t-статистика, сравнивается с критической точкой распределения Стьюдента, находящееся в строке t критическое двухстороннее (для двухсторонней критической области), а затем принимается решение согласно указанному выше правилу. Практические задания
5.1. Оценка значимости результатов наблюдений в случае двух независимых выборок
Исследуется результат действия нового препарата на зрительную память человека. В одной группе испытуемых препарат не вводился, а в контрольной группе тест проведен после ведения данного препарата. Результаты теста в первой группе (хi) и в контрольной группе (уi) выглядят следующим образом:
Установить с уровнем значимости a=0,05, влияет ли данный препарат на зрительную память?
Для выполнения этого задания проделайте следующие пункты. 1. Наберите исходные данные в две колонки: 2. Сначала следует проверить гипотезу о равенстве генеральных дисперсий по критерию Фишера. Для этого выполните команду Сервис ® Анализ данных. 3. В появившемся диалоговом окне Анализ данных выберите среди инструментов анализа необходимый в данном случае Двухвыборочный F-тест для дисперсии и нажмите ОК. 4. В появившемся диалоговом окне Двухвыборочный F-тест для дисперсии поместите курсор в поле Интервал переменной 1 и введите в него адрес интервала ячеек с данными 5. Поместите курсор в поле Интервал переменной 2. Затем введите адрес интервала ячеек с данными 6. Проверьте, установлен ли необходимый вам уровень значимости a. По умолчанию в поле Альфа установлено значение 0,05. 7. В группе Параметры вывода активизируйте переключатель Выходной интервал и поместите курсор в ставшее активным (белым) поле ввода справа от него. Затем щелкните мышью по ячейке С1, тогда ее адрес появится в этом поле. Нажмите ОК. 8. В результате появится таблица с вычисленными значениями критерия Фишера. Сразу, не сбрасывая выделения с этой таблицы, выполните команду Формат ® Столбец ® Автоподбор ширины. Полученная таблица должна иметь вид:
9. В первой колонке этой таблицы находятся названия статистических характеристик, вычисленных данным Инструментом анализа. Во второй и третьей колонках содержатся их вычисленные значения для переменных хi и уi. 10. Из полученной таблицы следует, что средние 11. Воспользовавшись правилом принятия решения из §5.2. для критерия Фишера в случае двусторонней критической области, можно сделать вывод: поскольку выполняется соотношение 12. Теперь следует сравнить средние двух выборок. Поскольку с помощью F -теста установлено, что различие между дисперсиями этих выборок статистически недостоверно, то для сравнения средних следует использовать инструмент анализа Двухвыборочный t-тест с одинаковыми дисперсиями. 13. Для его вызова выполните команду Сервис ® Анализ данных, выделите нужный инструмент и нажмите ОК. 14. В появившемся диалоговом окне Двухвыборочный t-тест с одинаковыми дисперсиями заполните все необходимые поля точно также, как и в предыдущем случае в окне Двухвыборочный F-тест для дисперсии за исключением того, что в группе Параметры вывода в поле Выходной интервал укажите адрес ячейки С12. 15. После заполнения всех необходимых полей (оставьте пустым поле гипотетическая разность и не активизируйте переключатель метка), нажмите на ОК. В результате выполнения t -теста должна появиться таблица:
17. Структура этой таблицы примерно такая же, как и таблицы, появившейся после выполнения F -теста. После t -теста с одинаковыми дисперсиями, помимо выборочных средних и исправленных дисперсий выборок, вычисляются: дисперсия генеральной совокупности (Объединенная дисперсия) s2=2,178030303; число степеней свободы (4.4) распределения Стьюдента (df) k =22; наблюдаемой значение (4.3) критерия Стьюдента (t-статистика)
18. Воспользовавшись правилом принятия решения из §5.3. для критерия Стьюдента в случае двусторонней критической области, можно сделать вывод: поскольку выполняется соотношение
5.2. Сравнение выборочных средних двух зависимых выборок
В результаты семилетних испытаний ячменя и овса на урожайность получены следующие данные:
где xi – урожайность ячменя в ц/га и yi – урожайность овса в ц/га в i -ом году. Установить, являются ли эти результаты существенно различными?
Для выполнения этого задания проделайте следующие пункты. 1. Занесите исходные данные в две колонки: xi - в столбец А, yi -в столбец В. 2. Поскольку результаты испытаний связаны попарно, то следует использовать модифицированный критерий Стьюдента (парный t -тест для средних). 3. Выполните команду Сервис ® Анализ данных. В появившемся диалоговом окне Анализ данных выберите среди Инструментов анализа необходимый в данном случае Парный двухвыборочный t-тест для средних и нажмите ОК. 4. В появившемся диалоговом окне Парный двухвыборочный t-тест для средних в группе Входные данные поместите курсор в поле Интервал переменной 1. Затем введите адрес интервала ячеек с данными xi A1:A7, или выделите интервал с этими данными мышью, тогда адрес выделенного диапазона появится автоматически. 5. Поместите курсор в поле Интервал переменной 2. Затем введите адрес интервала ячеек с данными уi В1:В7, или выделите интервал с этими данными мышью, тогда адрес выделенного диапазона появится автоматически. 6. Проверьте, установлен ли необходимый вам уровень значимости a. По умолчанию в поле Альфа находится 0,05. 7. В группе Параметры вывода активизируйте переключатель Выходной интервал и поместите курсор в ставшее активным (белым) поле справа от него. Затем щелкните мышью по ячейке С1, тогда ее адрес появится в поле Выходного интервала. Нажмите ОК. 8. В результате появится таблица с вычисленными значениями выборочных средних, дисперсии, коэффициента корреляции и модифицированного критерия Стьюдента. Сразу, не сбрасывая выделения этой таблицы, выполните команду Формат ® Столбец ® Автоподбор ширины. Полученная таблица должна иметь вид:
9. В первой колонке этой таблицы находятся названия статистических характеристик, вычисленных данным Инструментом анализа. Во второй и третьей колонках содержатся вычисленные значения соответствующих статистических характеристик для переменных хi и уi. 10. Из полученной таблицы следует, что средние 11. Воспользовавшись правилом принятия решения из §5.4. для модифицированного критерия Стьюдента в случае двусторонней критической области, можно сделать вывод: поскольку выполняется соотношение
Задания для самостоятельного выполнения
1. Для сравнения точности двух станков-автоматов взяты две выборки. Результаты измерения контролируемого размера изделий
Можно ли считать с уровнем значимости a=0,1, что станки обладают одинаковой точностью? (Сравнить дисперсии). 2. В результате контрольных замеров содержания углерода в пробах нелегированной стали данной марки, производимой двумя предприятиями, получены данные:
где хi и уi - процентное содержание углерода в каждой пробе стали, произведенной соответственно на первом и втором предприятиях. Установить, значимо ли различается содержание углерода в нелегированной стали данной марки, производимой на этих предприятиях. (Сначала сравнить дисперсии, а затем средние). 3. Две экспертные группы проводили контрольные замеры процентного содержания азота в органических удобрениях:
Установить, является ли значимым различие контрольных замеров этих групп. (Сначала сравнить дисперсии, а затем средние).
4. С целью улучшения успеваемости студентов была разработана новая методика обучения основам менеджмента. Для проверки ее эффективности проводилось тестирование двух параллельных групп 1 курса (группы подобраны таким образом, что результаты тестирования до начала эксперимента в них были одинаковы, т.е. средний уровень успеваемости в этих группах одинаков). В первой группе новая методика обучения не применялась, а во второй группе обучение по этой методике проводилось в течение месяца. После данного периода обучения проведено тестирование, итоги которого имеют вид:
где хi - количество набранных каждым студентом баллов по тесту в первой группе и уi - во второй после периода обучения по новой методике. Установить, улучшилась ли успеваемость студентов после обучения по новой методике. (Сначала сравнить дисперсии, а затем средние). 5. Проведено исследование для определения влияния использования Internet на общую успеваемость студентов. В одной группе студентов в течение периода исследования студентам запрещалось пользоваться возможностями Internet, а в другой предлагалось ежедневно пользоваться средствами Internet не менее двух часов. После этого в обеих группах проведено тестирование, результаты которого имеют вид:
где хi и уi – результаты теста в баллах соответственно в первой и второй группах. Для уровня значимости a=0,02 установить, повлияло ли использование возможностей Internet на общую успеваемость в этих группах и в какую сторону? (Сначала сравнить дисперсии, а затем средние). 6. Лаборант при помощи двух различных приборов произвел в одном и том же порядке измерение дозы (в %) поглощенного излучения в пробах крови подопытного животного:
где xi - результаты измерений, полученные при помощи первого прибора, уi - результаты измерений, полученные при помощи второго прибора. Оценить, значимо ли различаются результаты измерений при помощи двух различных проборов. (Сравнить средние парным t -тестом). 7. В лаборатории в одном и том же порядке двумя разными методами произведен анализ процентного содержания некоторого вещества в костной ткани:
где xi - результаты измерения первым методом, уi - результаты измерения вторым методом. Сравнить два метода исследования. (Сравнить средние парным t -тестом).
Контрольные вопросы
1. Что называется статистической гипотезой, нулевой, альтернативной гипотезой? Какие бывают виды альтернативных гипотез? 2. Какие бывают виды ошибок при проверки статистических гипотез и что называется уровнем значимости? 3. Что такое статистический критерий? 4. Что называется критической областью и какие они бывают? 5. Сформулируйте основное правило принятия решения. 6. Что такое критерий Фишера, для чего он предназначен. Какое правило принятия решения для него? 7. Опишите последовательность действий для проведения F -теста в Excel. 8. Что такое критерий Стьюдента, для чего он предназначен, что нужно учитывать перед вычислениями критерия Стьюдента? 9. Какое правило принятия решения для критерия Стьюдента? 10. Опишите последовательность действий для проведения t -тестов в Excel и структуру появляющихся после этого таблиц с результатами. 11. В каком случае применяется модифицированный критерий Стьюдента? Сформулируйте правило принятия решения для этого критерия. 12. Опишите последовательность действий при проведении парного t -теста в Excel и структуру появляющейся после этого таблицы с результатами.
Рекомендуемая литература
1. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высш. Шк. 2000. 2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высш. Шк. 2000. 3. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: Юнити, 2001. 4. Лакин Г.Ф. Биометрия. М.: Наука, 1980. 5. Бейли Н. Математика в биологии и медицине. Пер. с англ. М.: Мир, 1970. 6. Колемаев В.А., Староверов О.В., Турундаевский В.Б. Теория вероятностей и математическая статистика. М.: Высш. Шк., 1991. 7. Боровков А.А. Теория вероятностей. М.: Наука, 1984. 8. Вентцель Е.С. Теория вероятностей. М.: Наука, 2000. 9. Гнеденко Б.В. Курс теории вероятностей. М.: Наука, 1988. 10. Гутер Р.С., Овчинский Б.В. Основы теории вероятностей. М., Просвещение, 1967. 11. Блатнер Патрик, Лори Анн Ульрих. Использование Microsoft Excel 2000. М.: Вильямс, 2000. 12. Додж М., Стинсон К. Эффективная работа с Excel 2000. С-П., 2000. 13. Уокенбах Дж. Microsoft Excel 2000. Библия пользователя. М.: Вильямс, 2000. 14. Рычков В. Самоучитель Excel 2000. С-П., 2000. 15. Кузьмичева Т.Г., Савотченко С.Е. Новые информационные технологии: электронные таблицы Excel. Белгород: Белаудит, 2000..
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1079; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.156.114 (0.012 с.) |

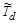 :
: - в столбец А,
- в столбец А,  - в столбец В.
- в столбец В. =10,16666667;
=10,16666667; 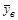 =8,25 (Среднее); исправленные дисперсии
=8,25 (Среднее); исправленные дисперсии  =2,333333333;
=2,333333333; 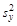 =2,022727273 (Дисперсия); объемы выборок (Наблюдения) n =12; числа степеней свободы (4.2) распределения Фишера (df) kх =11 и kу =11; наблюдаемое значение критерия Фишера (F)
=2,022727273 (Дисперсия); объемы выборок (Наблюдения) n =12; числа степеней свободы (4.2) распределения Фишера (df) kх =11 и kу =11; наблюдаемое значение критерия Фишера (F)  =1,153558052; критические точки распределения Фишера для заданного уровня значимости a=0,05 правосторонней критической области (F критическое одностороннее) F a(kх, kу)=2,817927225; вероятность того, что наблюдаемое значение критерия не попало в правостороннюю критическую область (P(F<=f) одностороннее) P (
=1,153558052; критические точки распределения Фишера для заданного уровня значимости a=0,05 правосторонней критической области (F критическое одностороннее) F a(kх, kу)=2,817927225; вероятность того, что наблюдаемое значение критерия не попало в правостороннюю критическую область (P(F<=f) одностороннее) P ( =3,18>2,07= t 0,05(22), то основная гипотеза отвергается. Это означает, что по измеряемому показателю новый препарат оказывает влияние на зрительную память.
=3,18>2,07= t 0,05(22), то основная гипотеза отвергается. Это означает, что по измеряемому показателю новый препарат оказывает влияние на зрительную память.


