
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило проверки гипотезы о законе распределения случайной величиныСодержание книги
Поиск на нашем сайте
Ранее отмечалось, что статистика c2 принимает только неотрицательные значения, причём в нуль она обращается в единственном случае – при совпадении эмпирических и теоретических частот. Если выдвинутая гипотеза о законе распределения изучаемой случайной величины соответствует действительности, то эмпирические и теоретические частоты должны быть примерно одинаковы, а значит, значения статистики c2 будут группироваться около нуля. Если же выдвинутая гипотеза ложна, то эмпирические и соответствующие теоретические частоты будут существенно разниться, что приведёт к достаточно большим отклонениям от нуля значений c2. Поэтому хотелось бы найти тот рубеж, называемый критическим значением (критической точкой) и обозначаемый через
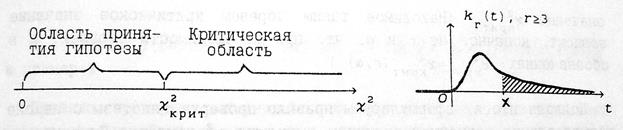
Рис. 4 Рис. 5 Если выдвинутая гипотеза о законе распределения изучаемой случайной величины верна, то вероятность попадания значений в критическую область должна быть мала, так что событие {
называется уровнем значимости. Чтобы определить критическое значение
с неизвестной х. Поскольку распределение статистики c2 близко при n®¥ к c2 -распределению с r степенями свободы, то
и приближённое значение
Последнее уравнение имеет единственное решение: его корень – это такое число х>0, при котором площадь под графиком функции kr(t) (плотности c2 -распределения) над участком [х; +¥) равна a (рис. 5). На практике решение последнего находят при помощи специальных таблиц, позволяющих по двум входным параметрам – уровню значимости a числу степеней свободы r определить критическое значение Подводя итоги, сформулируем правило проверки гипотезы о законе распределения случайной величины с помощью c2 -критерия Пирсона:
1) Проводят n независимых наблюдений случайной величины (принято считать, что должно быть n³100). 2) Разбивают всю числовую ось на несколько (как правило, на 8-12) промежутков так, чтобы количество результатов измерений в каждом из них (называемое эмпирической частотой ni) оказалось не менее пяти. 3) Выдвигают (например, судя по профилю гистограммы) гипотезу о законе распределения изучаемой случайной величины и находят параметры этого закона (чаще всего заменяя математическое ожидание и дисперсию их оценками). 4) С помощью предполагаемого (теоретического) распределения находят теоретические вероятности pi и теоретические частоты 5) По эмпирическим и теоретическим частотам вычисляют значение статистики c2,обозначаемое как 6) Определяют число r степеней свободы. 7) Используя заданное значение уровня значимости a и найденное число степеней свободы r, по таблице находят критическое значение 8) Формулируют вывод, опираясь на основной принцип проверки статистических гипотез ‑ если наблюдаемое значение критерия принадлежит критической области, то гипотезу отвергают как плохо согласующуюся с результатами эксперимента; ‑ если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают как не противоречащую результатам эксперимента.
|
|||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.93.183 (0.006 с.) |

 , который разбил бы всю область возможных значений статистики c2 на два непересекающихся подмножества (рис.4): область принятия гипотезы, характеризующуюся неравенством
, который разбил бы всю область возможных значений статистики c2 на два непересекающихся подмножества (рис.4): область принятия гипотезы, характеризующуюся неравенством 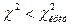 , и критическую область (или область отвержения гипотезы), определяющуюся неравенством
, и критическую область (или область отвержения гипотезы), определяющуюся неравенством  .
.
 ,
,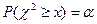

 .
.
 попадания значений случайной величины в i -й промежуток.
попадания значений случайной величины в i -й промежуток. .
.


